Chi-Square Tests

January 22, 2024.

  1. The chi-square test is a statistical test used to determine if there is a significant difference between the observed values and the expected values in a categorical data set.
  2. It measures the deviation between the expected and observed frequencies in one or more categories and assesses whether this deviation is statistically significant.
  3. The result of a chi-square test is a test statistic, and its p-value is compared against a threshold (e.g. \(\alpha = 0.05\)) to determine the statistical significance of the observed differences.
  4. The test is commonly used in hypothesis testing, contingency table analysis, and goodness-of-fit testing.

Types of Tests

  1. There are several types of chi-square tests. The most popular tests are as follows.
Test Use
A. Goodness-of-fit test determine if a sample of data fits a specified distribution
B. Independence test determine if there is a relationship between two categorical variables
  1. Additional chi-square tests include:
  • Homogeneity test: used to determine if different populations have the same distribution of a categorical variable.
  • Contingency table test: used to analyze the relationship between two or more categorical variables in a multi-dimensional table.
  • McNemar’s test: used to determine if the difference between paired nominal data is significant.
  • Likelihood-ratio test: used to compare nested models, where the more complex model is tested against a simpler model.
  • Mantel-Haenszel test: used to determine if there is a relationship between two categorical variables while controlling for the effect of a third variable.

Chi-Square Goodness of Fit test

A Business Application of the Chi-Square Goodness of Fit test

  1. Suppose a retail company wants to know if the gender distribution of their customer base is representative of the general population. They collect data on the gender of a sample of their customers and compare it to the expected distribution (e.g. 50% male and 50% female).
  2. The Chi-Square Goodness of Fit test is then used to evaluate the null hypothesis that the observed distribution of gender among the company’s customers is the same as the expected distribution.
  3. The test could help us potentially conclude that there is a significant difference between the observed and expected distributions, and the company’s customer base may not be representative of the general population.
  4. For example, the results might show that a significantly higher proportion of females than expected are customers of the company. This information could be used by the retail company to tailor their marketing strategies and product offerings to better attract male customers.

Concept

The Chi-Square Goodness-of-Fit test is a statistical tool used to determine if the observed data in a categorical dataset aligns with the expected data based on a particular hypothesis or anticipated distribution. It helps researchers evaluate if there exists a noteworthy difference between the actual data and what would be anticipated under a specific theoretical model or hypothesis.

Here are the essential steps and concepts involved in carrying out a Chi-Square Goodness-of-Fit test:

  1. Hypotheses:
    • Null Hypothesis (H0): The observed data conforms to a specific theoretical distribution.
    • Alternative Hypothesis (Ha): The observed data does not conform to the specified theoretical distribution.
  2. Categorical Data:
    • The data should be categorical, divided into distinct categories or groups.
    • We need both observed (actual) and expected frequencies for each category.
  3. Expected Frequencies:
    • Calculate the expected frequencies for each category based on the null hypothesis or the theoretical distribution. These expected values represent what we would anticipate seeing if the null hypothesis were accurate.
    • Expected frequencies can be computed using a formula or by multiplying the total sample size by the probabilities associated with each category according to the theoretical distribution.
  4. Chi-Square Statistic:

    • Determine the Chi-Square statistic using this formula:

      χ² = Σ ((O - E)² / E)

      • χ²: Chi-Square statistic
      • O: Observed frequency for a category
      • E: Expected frequency for the same category
      • Σ: The sum symbol, signifying that we should perform this calculation for all categories
  5. Degrees of Freedom (df):
    • The degrees of freedom for a Chi-Square Goodness-of-Fit test is equal to the number of categories minus one, or df = (number of categories - 1).
  6. Chi-Square Distribution:
    • The Chi-Square statistic follows a specific distribution known as the Chi-Square distribution, with df degrees of freedom.
  7. Critical Value and Significance Level:
    • Identify the critical value for the Chi-Square test at a chosen significance level (usually denoted as alpha). The critical value is typically derived from a Chi-Square distribution table or statistical software.
    • Common significance levels include 0.05 or 0.01.
  8. Statistic vs. Critical Value Comparison:
    • If the calculated Chi-Square statistic exceeds the critical value, we reject the null hypothesis.
    • If the calculated Chi-Square statistic is less than or equal to the critical value, we do not reject the null hypothesis.
  9. Interpretation:
    • Rejecting the null hypothesis implies a significant discrepancy between the observed data and the expected distribution, suggesting that the data does not adhere to the specified theoretical model.
    • Failing to reject the null hypothesis suggests no significant difference, indicating that the observed data aligns with the expected distribution.

In summary, the Chi-Square Goodness-of-Fit test serves to evaluate whether categorical data conforms to a particular theoretical distribution. It helps us assess whether any deviations from the expected distribution are statistically meaningful or simply due to chance.

Numerical Illustration

Business Scenario

We work for an e-commerce company that sells electronic gadgets. Our goal is to determine if the distribution of the company’s most popular product categories among customers aligns with the expected distribution based on last year’s market research. The expected distribution percentages are as follows:

  • Smartphones: 30%
  • Laptops: 40%
  • Accessories: 20%
  • Wearables: 10%

We aim to test if the observed distribution of product categories sold in a recent month matches this expected distribution.

Simulated Observed Data

The distribution of product categories sold in the recent month was observed as:

  • Smartphones: 25
  • Laptops: 42
  • Accessories: 18
  • Wearables: 15

Chi-Square Goodness-of-Fit Test

Step 1: Set up Hypotheses

  • Null Hypothesis (H0): The observed distribution matches the expected distribution.
  • Alternative Hypothesis (Ha): The observed distribution does not match the expected distribution.

Step 2: Organize Data

  • Expected Distribution:
    • Smartphones: 30%
    • Laptops: 40%
    • Accessories: 20%
    • Wearables: 10%
  • Observed Distribution:
    • Smartphones: 25
    • Laptops: 42
    • Accessories: 18
    • Wearables: 15

Step 3: Calculate Expected Frequencies

  • First, calculate the total number of products sold, which is the sum of the observed sales for all categories: 100.
  • Then, calculate the expected frequencies:
    • Expected Smartphones: 30 (100 * 30%)
    • Expected Laptops: 40 (100 * 40%)
    • Expected Accessories: 20 (100 * 20%)
    • Expected Wearables: 10 (100 * 10%)

Step 4: Calculate the Chi-Square Statistic

  • Use the formula: χ² = Σ ((O - E)² / E) for each category and then sum them up.
  • χ² = [(25 - 30)² / 30] + [(42 - 40)² / 40] + [(18 - 20)² / 20] + [(15 - 10)² / 10]
  • χ² = (25 / 30) + (4 / 40) + (4 / 20) + (25 / 10)
  • χ² ≈ 3.63 (rounded to two decimal places)

Step 5: Determine Degrees of Freedom (df)

  • df = (Number of Categories - 1) = 4 - 1 = 3

Step 6: Set Significance Level

  • Choose a significance level (alpha), e.g., 0.05.

Step 7: Find Critical Value

  • Using a Chi-Square distribution table or calculator for df = 3 and α = 0.05, the critical value is approximately 7.815.

Critical Value: This is a point on the scale of the test statistic beyond which we reject the null hypothesis, and it’s dependent on the chosen significance level (alpha, α) and the degrees of freedom in the test. In this case, χ² (critical) ≈ 7.815 is the critical value for a Chi-Square test with a significance level of 0.05 (5%) and degrees of freedom (df) equal to 3. This critical value is derived from the Chi-Square distribution table, which provides critical values for different levels of α and df.

Step 8: Compare Statistic to Critical Value

  • χ² (calculated) ≈ 3.63 < χ² (critical) ≈ 7.815

Step 9: Make a Decision

  • Since the calculated Chi-Square statistic (3.63) is less than the critical value (7.815), we fail to reject the null hypothesis.

Step 10: Interpretation

  • We conclude that there is no significant difference between the observed distribution of product categories sold and the expected distribution based on market research. In other words, the product categories sold match the expected distribution.

Running the Chi-Square Goodness of Fit Test in R

We present another example of running this test, this time using the mtcars data in R.

The primary goal is to use statistical methods to assess whether the actual distribution of gears in cars (as observed in the mtcars dataset) matches a set of expected probabilities, thereby validating or refuting assumptions about gear distribution in the dataset.

The set of expected probabilities for each gear category is as follows:

  • 0.5 or 50% for cars with 3 gears

  • 0.3 or 30% for cars with 4 gears

  • 0.2 or 20% for cars with 5 gears

This test is used to determine if there is a significant difference between observed frequencies (in this case, the number of cars with different gears) and expected frequencies.

1. Data Preparation

We start with the mtcars dataset, which contains information about 32 cars, each categorized with 3, 4, or 5 gears.

# Load the mtcars dataset
data(mtcars)

# Create a table to count the number of cars in each gear category
gear_counts <- table(mtcars$gear)
gear_counts

 3  4  5 
15 12  5

2. Visualization of Contingency Table

We visualize the contingency table using a graphical balloon plot:

# Load the gplots library for graphical plotting
library("gplots")

Attaching package: 'gplots'
The following object is masked from 'package:stats':

    lowess
# Convert gear counts into a table format
gear_table <- as.table(as.matrix(gear_counts))

# Create a graphical balloon plot
balloonplot(t(gear_table), main="Contingency Table",
            xlab="Gear",
            label=FALSE, show.margins=FALSE)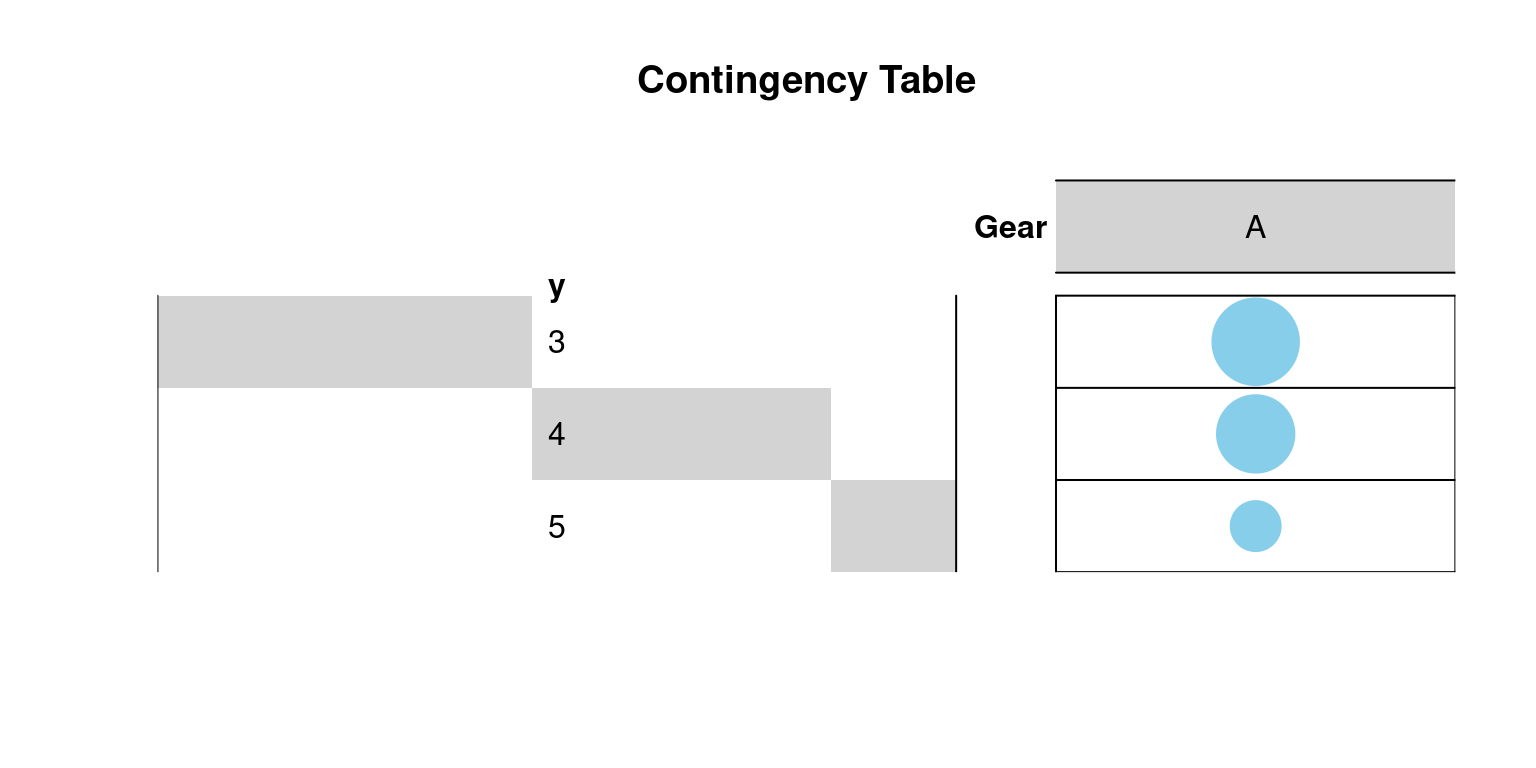

3. Calculation of Proportions

We calculate the proportions of cars in each gear category:

# Calculate proportions of cars in each gear category
gear_proportions <- prop.table(gear_counts)
gear_proportions

      3       4       5 
0.46875 0.37500 0.15625

4. Running the Chi-Square Goodness-of-Fit Test

We specify the expected probabilities for each gear category and perform the chi-square goodness-of-fit test:

# Specify the expected probabilities for each gear category
expected_probs <- c(0.5, 
                    0.3, 
                    0.2)

# Perform the chi-square goodness-of-fit test using observed proportions and expected probabilities
chisq_test_result <- chisq.test(gear_proportions, 
                                p=expected_probs)
chisq_test_result

    Chi-squared test for given probabilities

data:  gear_proportions
X-squared = 0.030273, df = 2, p-value = 0.985

5. Interpretation

After running the chi-square goodness-of-fit test using the provided expected probabilities, the output provides important information:

  • Chi-squared test for given probabilities: This line indicates that the test conducted is specifically a chi-square goodness-of-fit test. It’s designed to assess whether the observed data fits the expected probabilities we’ve provided.

  • data: gear_proportions: This line specifies the dataset used for the test, which is the gear_proportions dataset. This dataset contains the observed proportions of cars in different gear categories.

  • X-squared = 0.030273: This value represents the chi-square statistic (X²), which is a measure of how closely the observed proportions align with the expected probabilities. In this case, the calculated chi-square statistic is approximately 0.030273.

  • df = 2: This indicates the degrees of freedom (df) associated with the chi-square distribution. In a goodness-of-fit test like this one, the df is calculated as one less than the number of categories being analyzed. Here, since there are three gear categories (3, 4, and 5), df equals 2.

  • p-value = 0.985: The p-value is a crucial result of the test. It represents the probability of observing a chi-square statistic as extreme as the calculated value (0.030273) under the assumption that there is no significant difference between the observed and expected proportions. In this case, the high p-value of 0.985 suggests that the observed data aligns well with the expected probabilities. A high p-value implies that there is no strong evidence to reject the null hypothesis, which means that the data does not provide significant grounds to believe that the observed proportions are different from what was expected.

In summary, this output tells us that the chi-square goodness-of-fit test was conducted using the observed proportions of cars in different gear categories and the specified expected probabilities. The resulting high p-value (0.985) indicates that there is no strong reason to conclude that the observed proportions significantly differ from the expected probabilities, thus failing to reject the null hypothesis.

Comparison of Chi-Square Goodness of Fit test with Z-test for Proportions

The Chi-Square Goodness of Fit test is employed to assess whether observed data conforms to an expected distribution, particularly when dealing with categorical data. It evaluates the similarity between observed and expected frequencies across different categories, typically through a chi-square statistic and follows a chi-square distribution.

It is used when you have categories or groups, and it helps determine if the observed data matches an expected distribution within those categories. It’s like checking if things are divided as you’d expect.

In contrast, the Z-test for Proportions focuses on comparing a sample proportion with a known population proportion, typically in binary data scenarios. It uses a Z-score to measure the difference and follows a standard normal distribution.

It helps us assess if the proportion of “yes” responses in our sample significantly differs from a known or expected proportion. It’s like comparing one group to a known standard.

Chi-Square Test of Independence

A Business Application of the Chi-Square Test of Independence

  1. Suppose a grocery store wants to evaluate the association between the type of product a customer buys and their age group.
  2. Suppose the grocery store wants to know if there is a significant association between the type of product a customer buys (e.g. fruits, vegetables, or dairy products) and their age group (e.g. 18-30, 31-45, 46-60, 61 and older). They collect data on the age group and product type for a sample of customers and create a contingency table.
  3. The Chi-square test is then used to evaluate the null hypothesis that the product type and age group are independent.
  4. Depending on the test result, we could potentially conclude that there is a significant association between the two variables.
  5. For example, the results might show that a significantly higher proportion of customers in the 46-60 age group buy fruits compared to the other age groups.
  6. This information could be used by the grocery store to adjust their marketing strategies and product offerings to better cater to their target customers.

Chi-Square Test of Independence – Technicalities

  1. The Chi-square test of independence is a statistical test used to determine if there is a significant association between two categorical variables.
  2. The test evaluates the null hypothesis that the two variables are independent and calculates a test statistic (chi-square) based on the difference between the observed and expected frequencies of the two variables.
  3. If the calculated test statistic is larger than the critical value from a chi-square distribution table, then the null hypothesis is rejected and it can be concluded that there is a significant association between the two variables.

Running the Chi-Square Test of Independence Test in R

The overall objective of this test is to qualitatively and quantitatively analyze and understand the interrelationships between different categorical variables in the mtcars dataset.

Specifically, in this illustration, the test aims to explore the association between the number of cylinders (cyl) and transmission type (am), in the dataset.

  1. Convert the categorical variables into factor variables in the dataset mtcars.

This step ensures that R treats these variables as categorical data, which is necessary for a Chi-Square test.

data(mtcars)
mtcars$cyl <- as.factor(mtcars$cyl)
mtcars$am  <- as.factor(mtcars$am)
mtcars$gear  <- as.factor(mtcars$gear)
  1. Creating a Contingency Table:
ctab <- table(mtcars$am, 
              mtcars$cyl)
ctab
   
     4  6  8
  0  3  4 12
  1  8  3  2

A contingency table (ctab) is created to summarize the relationship between two categorical variables.

  1. Graphical display of Contingency table:

The balloonplot function from the gplots library is used to visually represent the contingency table.

library("gplots")
# 1. convert the data as a table
dt <- as.table(
  as.matrix(ctab))

# 2. Graph
balloonplot(t(dt), 
            main ="Contingency Table",
            xlab ="cyl", ylab="am",
            label = FALSE, 
            show.margins = FALSE)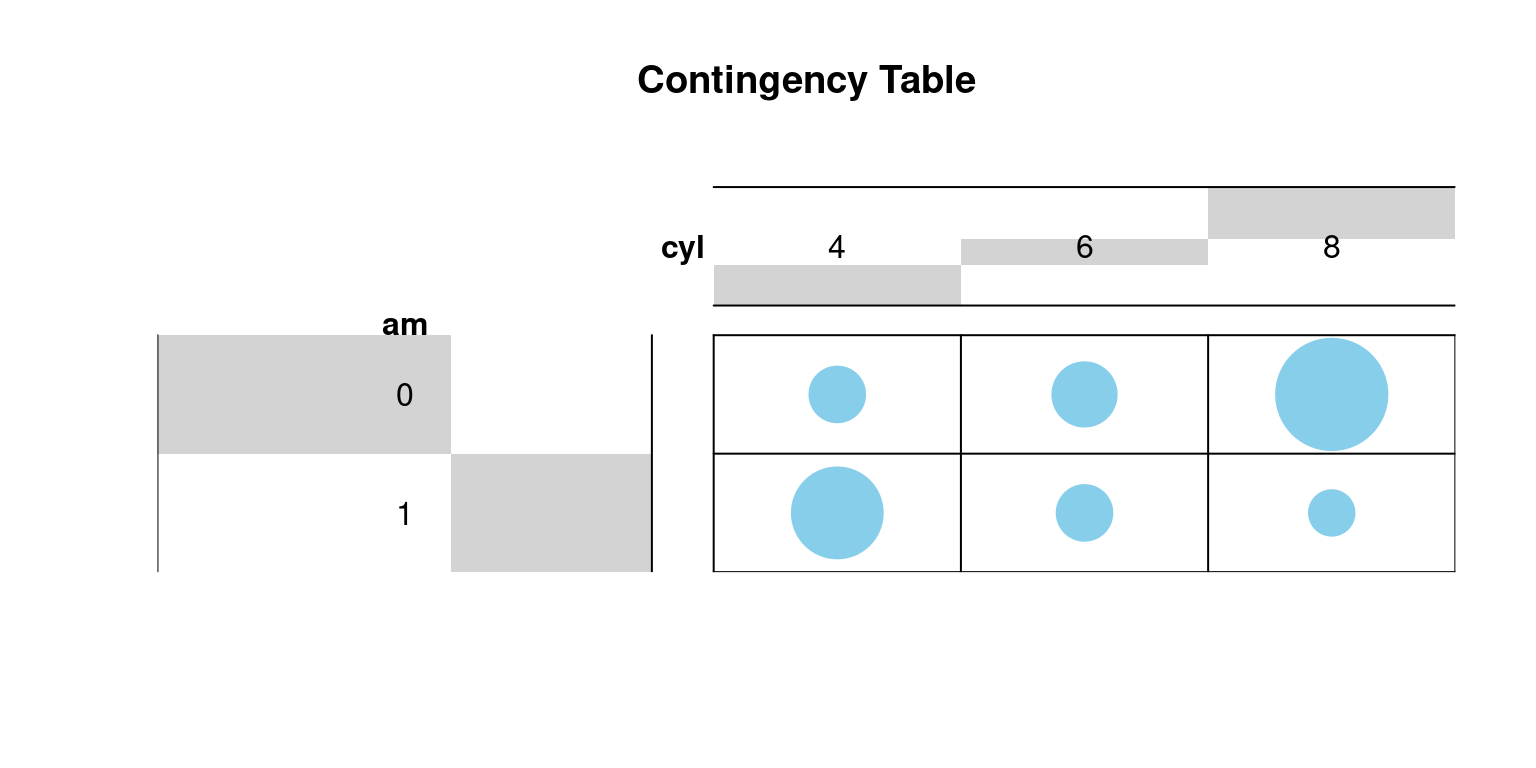

  1. Compute Chi-Square test: The Chi-square statistic can be easily computed using the function chisq.test() as follow:
chisq <- chisq.test(ctab)
Warning in chisq.test(ctab): Chi-squared approximation may be incorrect
chisq

    Pearson's Chi-squared test

data:  ctab
X-squared = 8.7407, df = 2, p-value = 0.01265

  1. In our example, the row and the column variables are statistically significantly associated (p-value = 0.01265). This indicates a statistically significant association between the variables at common alpha levels (like 0.05).

  2. The observed and the expected counts can be extracted from the result of the test as follows:

# Observed counts
chisq$observed
   
     4  6  8
  0  3  4 12
  1  8  3  2
# Expected counts
round(chisq$expected, 2)
   
       4    6    8
  0 6.53 4.16 8.31
  1 4.47 2.84 5.69
  1. Pearson Residuals:

Positive residuals are positive values in cells specify an attraction (positive association) between the corresponding row and column variables.

Negative residuals implies a repulsion (negative association) between the corresponding row and column variables.

round(chisq$residuals, 3)
   
         4      6      8
  0 -1.382 -0.077  1.279
  1  1.670  0.093 -1.546

The overall qualitative objective of running the Chi-Square Test of Independence, as described in the example using the mtcars dataset in R, is to determine whether there is a statistically significant relationship between different categorical variables in the dataset. Specifically, the test aims to explore the association between variables like the number of cylinders (cyl), transmission type (am), in the dataset. The key goals and insights sought from this test include:

  1. Understanding Relationships Between Variables: To identify if there is a statistically significant association between different categorical variables in the dataset. For instance, it might reveal whether the type of transmission (automatic or manual) is associated with the number of cylinders or gears in the cars.

  2. Testing Hypotheses About Associations: The Chi-Square Test of Independence is essentially a hypothesis test. The null hypothesis states that there is no association between the variables (they are independent), while the alternative hypothesis suggests there is an association (they are not independent).

  3. Guiding Data-Driven Decisions: By understanding the relationships between variables, businesses, analysts, or data scientists can make informed decisions. For example, if a significant association is found between certain car features, it might influence marketing strategies or product development.

  4. Visualizing Data Relationships: Through graphical representation like balloon plots, the test provides a visual understanding of the strength and nature of the relationships between categorical variables.

  5. Quantitative Analysis of Associations: Beyond just identifying if an association exists, the test provides measures like the chi-square statistic, p-value, observed and expected counts, and Pearson residuals. These measures quantify the strength of association and help in understanding the nature of the relationship (whether it’s positive or negative).

The overall objective of this test is to qualitatively and quantitatively analyze and understand the interrelationships between different categorical variables in the mtcars dataset.

References

[1] Agresti, A. (2002). Categorical data analysis (2nd ed.). Wiley.

Hair Jr, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2010). Multivariate data analysis: A global perspective (7th ed.). Pearson Education.

Everitt, B. S. (1992). The analysis of contingency tables (2nd ed.). Chapman and Hall.