Bivariate Continuous data (Part 1 of 4)

Chapter 12.

  1. This chapter explores Categorical x Continuous data. It explains how to summarize and visualize bivariate continuous data across categories. Here, we delve into the intersection of continuous data and categorical variables, examining how continuous data can be split, summarized, and compared across different levels of one or more categorical variables.

  2. We bring to light methods for generating statistics per group and data manipulation techniques. This includes processes like grouping, filtering, and summarizing continuous data, contingent on categorical variables. We visualize such data by creating juxtaposed box plots, segmented histograms, and density plots that reveal the distribution of continuous data across varied categories.

  3. Data: Suppose we run the following code to prepare the mtcars data for subsequent analysis and save it in a tibble called tb. [1]

# Load the required libraries, suppressing annoying startup messages
library(dplyr, quietly = TRUE, warn.conflicts = FALSE)
library(tibble, quietly = TRUE, warn.conflicts = FALSE)
library(knitr) # For formatting tables

# Read the mtcars dataset into a tibble called tb
data(mtcars)
tb <- as_tibble(mtcars)

# Convert relevant columns into factor variables
tb$cyl <- as.factor(tb$cyl) # cyl = {4,6,8}, number of cylinders
tb$am <- as.factor(tb$am) # am = {0,1}, 0:automatic, 1: manual transmission
tb$vs <- as.factor(tb$vs) # vs = {0,1}, v-shaped engine, 0:no, 1:yes
tb$gear <- as.factor(tb$gear) # gear = {3,4,5}, number of gears

# Directly access the data columns of tb, without tb$mpg
attach(tb)

Summarizing Continuous Data

Across one Category

  • We review the use of the inbuilt functions (i) aggregate(); (ii) tapply(); and the function (iii) describeBy() from package pysch, to summarize continuous data split across a category.
  1. Using aggregate()
  • We use the aggregate() function to investigate the bivariate relationship between mileage (mpg) and number of cylinders (cyl). The following code displays a summary table showing the average mileage of the cars broken down by number of cylinders (cyl = 4, 6, 8) using aggregate(). [1] [2]
# Aggregating 'mpg' column by the 'cyl' column.
# The aggregation function used is 'mean' to calculate the average.
A0 <- aggregate(tb$mpg, 
                by = list(tb$cyl), 
                FUN = mean)

# Renaming the column names of the aggregated data frame 'A0'.
# 'Cylinders' for the first column and 'Mean_mpg' for the second.
names(A0) <- c("Cylinders", "Mean_mpg")

# Displaying the aggregated data using 'kable' from the knitr package.
# Setting the number of digits to 2 for formatting and adding a caption.
kable(A0, digits=2, 
      caption = "Mean of Mileage (mpg) by Cylinder (cyl=4,6,8)")
Mean of Mileage (mpg) by Cylinder (cyl=4,6,8)
Cylinders Mean_mpg
4 26.66
6 19.74
8 15.10
  1. Discussion:

  • The first argument in aggregate() is the data vector tb$mpg.

  • The second argument, by, denotes a list of variables to group by. Here, we have supplied tb$cyl, since we wish to partition our data based on the unique values of cyl.

  • The third argument, FUN, is the function we want to apply to each subset of data. We are using mean here, calculating the average mpg for each unique cyl value. We can alternately aggregate based on a variety of statistical functions including sum, median, min, max, sd, var, length, IQR.

  • The output of aggregate() is saved in a new tibble named agg. We utilize the names() function to rename the columns and display agg. [1]

  1. Using tapply()
  • The tapply() function is another convenient tool to apply a function to subsets of a vector, grouped by some factors.
# Applying the 'mean' function to the 'mpg' column,
# grouping the data by the 'cyl' column
# The 'tapply' function applies a function to each cell.
A1 <- tapply(tb$mpg, 
             tb$cyl, 
             mean)
print(A1)
       4        6        8 
26.66364 19.74286 15.10000
  1. Discussion:

  • In this code, tapply(tb$mpg, tb$cyl, mean) calculates the average miles per gallon (mpg) for each unique number of cylinders (cyl) within the tb tibble.

  • tb$mpg represents the vector to which we want to apply the function.

  • tb$cyl serves as our grouping factor.

  • mean is the function that we’re applying to each subset of our data.

  • The result will be a vector where each element is the average mpg for a unique number of cylinders (cyl), as determined by the unique values of tb$cyl. [1]

  1. Using describeBy() from package psych
  • The describeBy() function, part of the psych package, can be used to compute descriptive statistics of a numeric variable, broken down by levels of a grouping variable. [3]
# Loading the 'psych' package
library(psych)

# Using the 'describeBy' from the 'psych' package for descriptive
# statistics of 'mpg' grouped by 'cyl'. 
A2 <- describeBy(mpg, cyl)
print(A2)

 Descriptive statistics by group 
group: 4
   vars  n  mean   sd median trimmed  mad  min  max range skew kurtosis   se
X1    1 11 26.66 4.51     26   26.44 6.52 21.4 33.9  12.5 0.26    -1.65 1.36
------------------------------------------------------------ 
group: 6
   vars n  mean   sd median trimmed  mad  min  max range  skew kurtosis   se
X1    1 7 19.74 1.45   19.7   19.74 1.93 17.8 21.4   3.6 -0.16    -1.91 0.55
------------------------------------------------------------ 
group: 8
   vars  n mean   sd median trimmed  mad  min  max range  skew kurtosis   se
X1    1 14 15.1 2.56   15.2   15.15 1.56 10.4 19.2   8.8 -0.36    -0.57 0.68
  1. Discussion:

  • describeBy(mpg, cyl) computes descriptive statistics of miles per gallon mpg variable, broken down by the unique values in the number of cylinders (cyl).

  • It calculates statistics such as the mean, sd, median, for mpg, separately for each unique number of cylinders (cyl). [3]

Across two Categories

  • We extend the above discussion and study how to summarize continuous data split across two categories.

  • We review the use of the inbuilt functions (i) aggregate() and the function (ii) describeBy() from package pysch. While the tapply() function can theoretically be employed for this task, the resulting code tends to be long and lacks efficiency. Therefore, we opt to exclude it from practical use.

  1. Using aggregate()
  • Distribution of Mileage (mpg) by Cylinders (cyl = {4,6,8}) and Transmisson Type (am = {0,1}) [1]
# Aggregating 'mpg' column by both 'cyl' and 'am' columns.
# The aggregation function used is 'mean'.
B0 <- aggregate(tb$mpg, 
                by = list(tb$cyl, tb$am),
                FUN = mean)

# Renaming the column names of the aggregated data frame 'B0'.
# 'Cylinders' 'Transmission'  'Mean_mpg' .
names(B0) <- c("Cylinders", "Transmission", "Mean_mpg")

# Displaying the aggregated data using 'kable' from the knitr package.
# Setting the number of digits to 2 for formatting and adding a caption.
kable(B0, 
      digits=2, 
      caption = "Mean of Mileage (mpg) by Cylinders and Transmission")
Mean of Mileage (mpg) by Cylinders and Transmission
Cylinders Transmission Mean_mpg
4 0 22.90
6 0 19.12
8 0 15.05
4 1 28.08
6 1 20.57
8 1 15.40
  1. Discussion:

  • In our code, the first argument of aggregate() is tb$mpg, indicating that we want to perform computations on the mpg variable.

  • The by argument is a list of variables by which we want to group our data, specified as list(tb$cyl, tb$am). This means that separate computations are done for each unique combination of cyl and am.

  • The FUN argument indicates the function to be applied to each subset of our data. Here, we use mean, meaning that we compute the mean mpg for each group. [1]

  1. Using aggregate() for multiple continuous variables: Consider this extension of the above code for calculating the mean of three variables - mpg, wt, and hp, grouped by both am and cyl variables:
  • Distribution of Mileage (mpg), Weight (wt), Horsepower (hp) by Cylinders (cyl = {4,6,8}) and Transmisson Type (am = {0,1})
# Aggregating mpg, wt, hp by 'am' and 'cyl' columns.
# The 'mean' function is used to calculate the average 
B1 <- aggregate(list(mpg, wt, hp), 
                by = list(am, cyl),
                FUN = mean)

# Renaming the column names of the aggregated data frame
names(B1) <- c("Transmission", "Cylinders", 
               "Mean_mpg", "Mean_wt", "Mean_hp")

# Displaying the aggregated data using 'kable' from the knitr package.
# Formatting numbers to two decimal places and adding a descriptive caption.
kable(B1, 
      digits=2, 
      caption = "Mean of mpg, wt, hp by am, cyl")
Mean of mpg, wt, hp by am, cyl
Transmission Cylinders Mean_mpg Mean_wt Mean_hp
0 4 22.90 2.94 84.67
1 4 28.08 2.04 81.88
0 6 19.12 3.39 115.25
1 6 20.57 2.76 131.67
0 8 15.05 4.10 194.17
1 8 15.40 3.37 299.50
  1. Discussion:

  • In this code, the aggregate() function takes a list of the three variables as its first argument, indicating that the mean should be calculated for each of these variables separately within each combination of am and cyl.

  • The sequence of the categorizing variables also varies - initially, the data is grouped by cyl, followed by a subdivision based on am.

  1. Using aggregate() with multiple functions: Consider an extension of the above code for calculating the mean and the SD of mpg, grouped by both am and cyl factor variables:
  • Distribution of Mileage (mpg), by Cylinders (cyl = {4,6,8}) and Transmission Type (am = {0,1}) [1]
# Calculating the mean of 'mpg' grouped by 'cyl' and 'am'.
agg_mean <- aggregate(tb$mpg, 
                      by = list(tb$cyl, tb$am), 
                      FUN = mean)

# Calculating the standard deviation (sd) of 'mpg'  by 'cyl' and 'am'.
agg_sd <- aggregate(tb$mpg, 
                    by = list(tb$cyl, tb$am), 
                    FUN = sd)

# Calculating the median of 'mpg' for each group of 'cyl' and 'am'.
agg_median <- aggregate(tb$mpg, 
                        by = list(tb$cyl, tb$am), 
                        FUN = median)

# Merging the mean and sd data frames based on 'cyl' and 'am'.
B2 <- merge(agg_mean, agg_sd, 
            by = c("Group.1", "Group.2"))

# Merging the above result 
B2 <- merge(B2, agg_median, 
            by = c("Group.1", "Group.2"))

# Renaming the columns of the merged data
names(B2) <- c("Cylinders", "Transmission", 
               "Mean_mpg", "SD_mpg", "Median_mpg")

# Displaying the merged data 
kable(B2, 
      digits=2, caption = "Mean, SD, Median of Mileage (mpg) 
      by Cylinders (cyl=4,6,8) and Transmission (am=0,1)")
Mean, SD, Median of Mileage (mpg) by Cylinders (cyl=4,6,8) and Transmission (am=0,1)
Cylinders Transmission Mean_mpg SD_mpg Median_mpg
4 0 22.90 1.45 22.80
4 1 28.08 4.48 28.85
6 0 19.12 1.63 18.65
6 1 20.57 0.75 21.00
8 0 15.05 2.77 15.20
8 1 15.40 0.57 15.40
  1. Discussion:

  • We analyze our dataset to comprehend the relationships between vehicle miles per gallon (mpg), number of cylinders (cyl), and type of transmission (am).

  • Initially, we computed the mean, standard deviation, and median of mpg for every unique combination of cyl and am.

  • After individual computations, we combined these results into a single, comprehensive data frame called merged_data. This structured dataset now clearly presents the average, variability, and median of fuel efficiency segmented by cylinder count and transmission type. [1]

  1. Using describeBy() from package psych
  • The describeBy() function, part of the psych package, can be used to compute descriptive statistics of continuous variable, broken down by levels of a two categorical varaibles. Consider the following code:
# Selecting specific columns ('mpg', 'wt', 'hp') 
tb_columns <- tb[c("mpg", "wt", "hp")]

# Creating a list of factors ('am' and 'cyl') for grouping in describeBy.
tb_factors <- list(tb$am, tb$cyl)

# Using the 'describeBy' function to provide  descriptive statistics 
# grouped by 'am' and 'cyl'.
B3 <- describeBy(tb_columns, 
                 tb_factors)

print(B3)

 Descriptive statistics by group 
: 0
: 4
    vars n  mean    sd median trimmed  mad   min   max range  skew kurtosis
mpg    1 3 22.90  1.45  22.80   22.90 1.93 21.50 24.40  2.90  0.07    -2.33
wt     2 3  2.94  0.41   3.15    2.94 0.06  2.46  3.19  0.73 -0.38    -2.33
hp     3 3 84.67 19.66  95.00   84.67 2.97 62.00 97.00 35.00 -0.38    -2.33
       se
mpg  0.84
wt   0.24
hp  11.35
------------------------------------------------------------ 
: 1
: 4
    vars n  mean    sd median trimmed   mad   min    max range  skew kurtosis
mpg    1 8 28.08  4.48  28.85   28.08  4.74 21.40  33.90 12.50 -0.21    -1.66
wt     2 8  2.04  0.41   2.04    2.04  0.36  1.51   2.78  1.27  0.35    -1.15
hp     3 8 81.88 22.66  78.50   81.88 20.76 52.00 113.00 61.00  0.14    -1.81
      se
mpg 1.59
wt  0.14
hp  8.01
------------------------------------------------------------ 
: 0
: 6
    vars n   mean   sd median trimmed  mad    min    max range  skew kurtosis
mpg    1 4  19.12 1.63  18.65   19.12 1.04  17.80  21.40  3.60  0.48    -1.91
wt     2 4   3.39 0.12   3.44    3.39 0.01   3.21   3.46  0.25 -0.73    -1.70
hp     3 4 115.25 9.18 116.50  115.25 9.64 105.00 123.00 18.00 -0.09    -2.33
      se
mpg 0.82
wt  0.06
hp  4.59
------------------------------------------------------------ 
: 1
: 6
    vars n   mean    sd median trimmed  mad    min    max range  skew kurtosis
mpg    1 3  20.57  0.75  21.00   20.57 0.00  19.70  21.00  1.30 -0.38    -2.33
wt     2 3   2.76  0.13   2.77    2.76 0.16   2.62   2.88  0.25 -0.12    -2.33
hp     3 3 131.67 37.53 110.00  131.67 0.00 110.00 175.00 65.00  0.38    -2.33
       se
mpg  0.43
wt   0.07
hp  21.67
------------------------------------------------------------ 
: 0
: 8
    vars  n   mean    sd median trimmed   mad    min    max range  skew
mpg    1 12  15.05  2.77  15.20   15.10  2.30  10.40  19.20  8.80 -0.28
wt     2 12   4.10  0.77   3.81    4.04  0.41   3.44   5.42  1.99  0.85
hp     3 12 194.17 33.36 180.00  193.50 40.77 150.00 245.00 95.00  0.28
    kurtosis   se
mpg    -0.96 0.80
wt     -1.14 0.22
hp     -1.44 9.63
------------------------------------------------------------ 
: 1
: 8
    vars n   mean    sd median trimmed   mad    min    max range skew kurtosis
mpg    1 2  15.40  0.57  15.40   15.40  0.59  15.00  15.80   0.8    0    -2.75
wt     2 2   3.37  0.28   3.37    3.37  0.30   3.17   3.57   0.4    0    -2.75
hp     3 2 299.50 50.20 299.50  299.50 52.63 264.00 335.00  71.0    0    -2.75
      se
mpg  0.4
wt   0.2
hp  35.5
  1. Discussion:

  • We specify a subset of the dataframe tb that includes only the columns of interest – mpg, wt, and hp and save it into a variable tb_columns.

  • Next, we create a list, tb_factors, that contains the factors am and cyl.

  • After that, we call the describeBy() function from the psych package. This function calculates descriptive statistics for each combination of levels of the factors am and cyl and for each of the continuous variables mpg, wt, and hp. [3]

Visualizing Continuous Data

Let’s take a closer look at some of the most effective ways of visualizing univariate continuous data, including

  1. Bee Swarm plots;

  2. Stem-and-Leaf plots;

  3. Histograms;

  4. PDF and CDF Density plots;

  5. Box plots;

  6. Violin plots;

  7. Q-Q plots.

Bee Swarm Plot

  1. We extend a Bee Swarm plot of a one-dimensional scatter plot for a continuous variable, split by a categorical variable. [4]

  2. Consider the following code, which generates a beeswarm plot displaying vehicle weights (wt) segmented by their number of cylinders (cyl):

# Loading the 'beeswarm' package
library(beeswarm)

# Creating a bee swarm plot of the 'wt' (weight) column, 
# grouped by the 'cyl' (cylinders) column. 
beeswarm(tb$wt ~ tb$cyl, 
         main="Bee Swarm Plot of Weight (wt) by Cylinders (cyl=4,6,8)", 
         xlab="Number of Cylinders",  # Label for the x-axis
         ylab="Weight ('000 kg)",     # Label for the y-axis
         pch=16,  # Type of points used in the plot (solid circle)
         cex=0.8, # Size of the points
         col=c("blue","red","darkgreen"),  # Colors for different groups
         horizontal = TRUE) # Orientation of the plot (horizontal)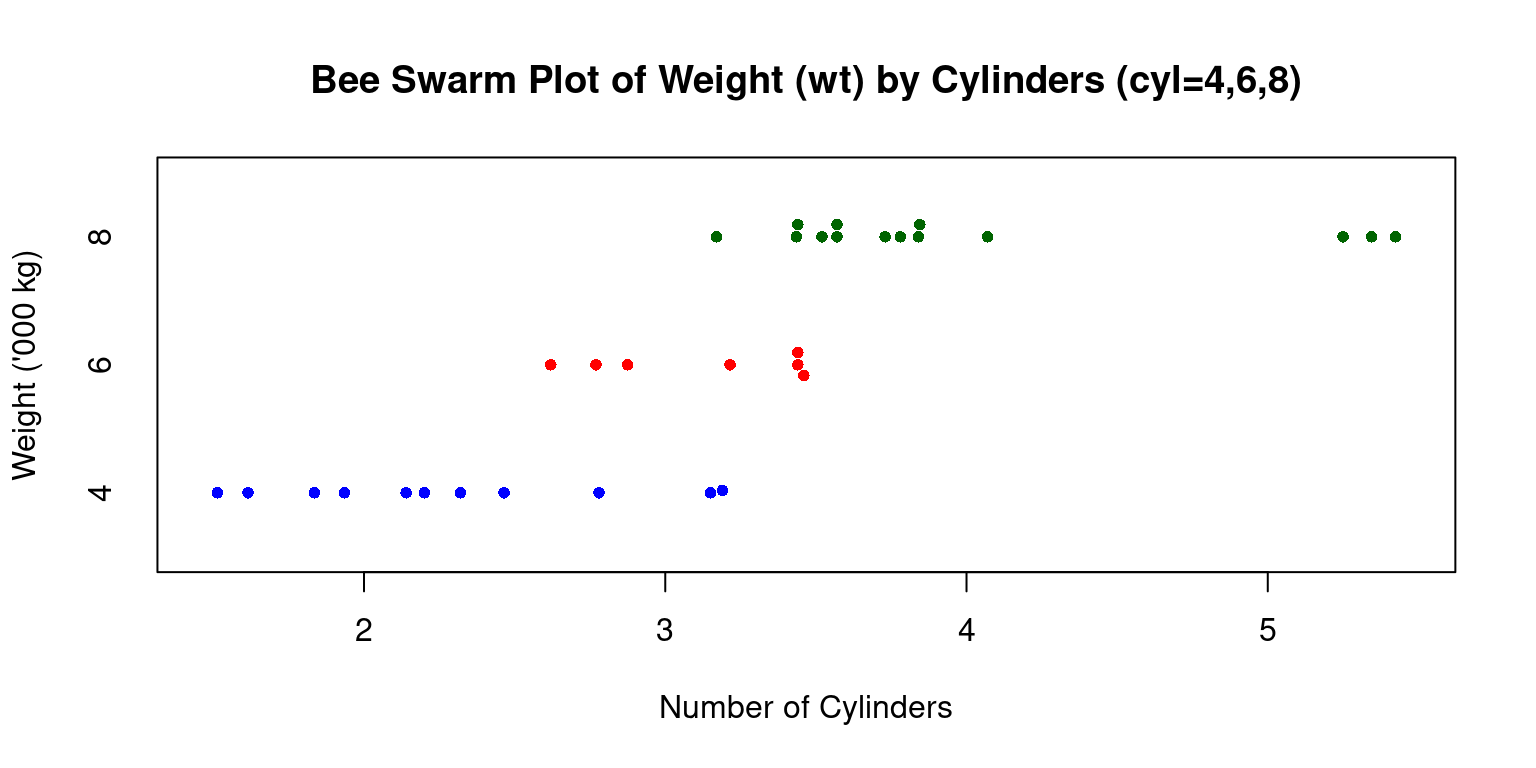

  1. Discussion:

  • Data: We use tb\(wt ~ tb\)cyl to specify that we want a beeswarm plot for Weight (wt), split by no of cylinders (cyl),

  • Title: It is labeled “Bee Swarm Plot of Weight (wt) by Number of Cylinders”.

  • Axes Labels: The x-axis shows “Number of Cylinders”, while the y-axis denotes “Weight (’000 kg)”.

  • Data Points: Using pch=16, data points appear as solid circles.

  • Size of Points: With cex=0.8, these circles are slightly smaller than default.

  • Colors: The col parameter assigns colors (“blue”, “red”, and “dark green”) based on cylinder counts.

  • Orientation: Set as horizontal with horizontal=TRUE.

  • To summarize, this visual distinguishes vehicle weights across cylinder counts and highlights data point densities for each group. [4]

Stem-and-Leaf Plot across one Category

  1. Suppose we wanted to visualize the distribution of a continuous variable across different levels of a categorical variable, using stem-and-leaf plots.

  2. To illustrate, let us display vehicle weights (wt) separately for each transmission type (am) using stem-and-leaf plots.

# Selecting 'wt' and 'am' columns from the 'tb' dataframe 
tb3 <- tb[, c("wt", "am")]

# Splitting the 'tb3' dataframe into subsets based on the 'am' column.
tb_split <- split(tb3, tb3$am)

# Applying a function to each subset in 'tb_split' using 'lapply'.
# Create a stem-and-leaf plot for the 'wt' column in each subset.
lapply(tb_split, 
       function(x) stem(x$wt))

  The decimal point is at the |

  2 | 5
  3 | 22244445567888
  4 | 1
  5 | 334


  The decimal point is at the |

  1 | 5689
  2 | 123
  2 | 6889
  3 | 2
  3 | 6
$`0`
NULL

$`1`
NULL
  1. Discussion:

  • Column Selection: The code extracts the wt (weight) and am (transmission type) columns from tb and saves them in tb3.

  • Data Splitting: It then divides tb3 into subsets based on am values, resulting in separate groups for each transmission type.

  • Visualization: Using lapply(), the code generates stem-and-leaf plots for the wt values in each subset, showcasing weight distributions for different transmission types. In this context, it shows the distribution of vehicle weights for each transmission type (automatic and manual). [5]

Histograms across one Category

  1. Visualizing histograms of car mileage (mpg) broken down by transmission (am=0,1)
split_data <- split(tb$mpg, tb$am) # Split the data by 'am' variable
# Splitting the 'mpg' data from the 'tb' dataframe by the 'am' variable.
split_data <- split(tb$mpg, tb$am)

# Setting up the graphics layout for two plots side by side.
par(mfrow = c(1, 2))

# Defining a color vector for use in the histograms.
color_vector <- c("skyblue", "gold")

# Creating a histogram for the subset with 'am' equals 0.
hist(split_data[[1]], 
     main = "Histogram of mpg (am = 0)", 
     breaks = seq(10, 35, by = 5), #  bin ranges (10-15, 15-20, etc.)
     xlab = "Miles per gallon", 
     col = color_vector[1], # Applying the first color
     border = "black", # Setting the border color of the bins.
     ylim = c(0, 10)) # Setting y-axis limits.

# Creating a histogram for the subset with 'am' equals 1.
hist(split_data[[2]], 
     main = "Histogram of mpg (am = 1)", 
     breaks = seq(10, 35, by = 5), #  bin ranges (10-15, 15-20, etc.)
     xlab = "Miles per gallon", 
     col = color_vector[2], # Applying the second color 
     border = "black", # Setting the border color of the bins.
     ylim = c(0, 10)) # Setting y-axis limits.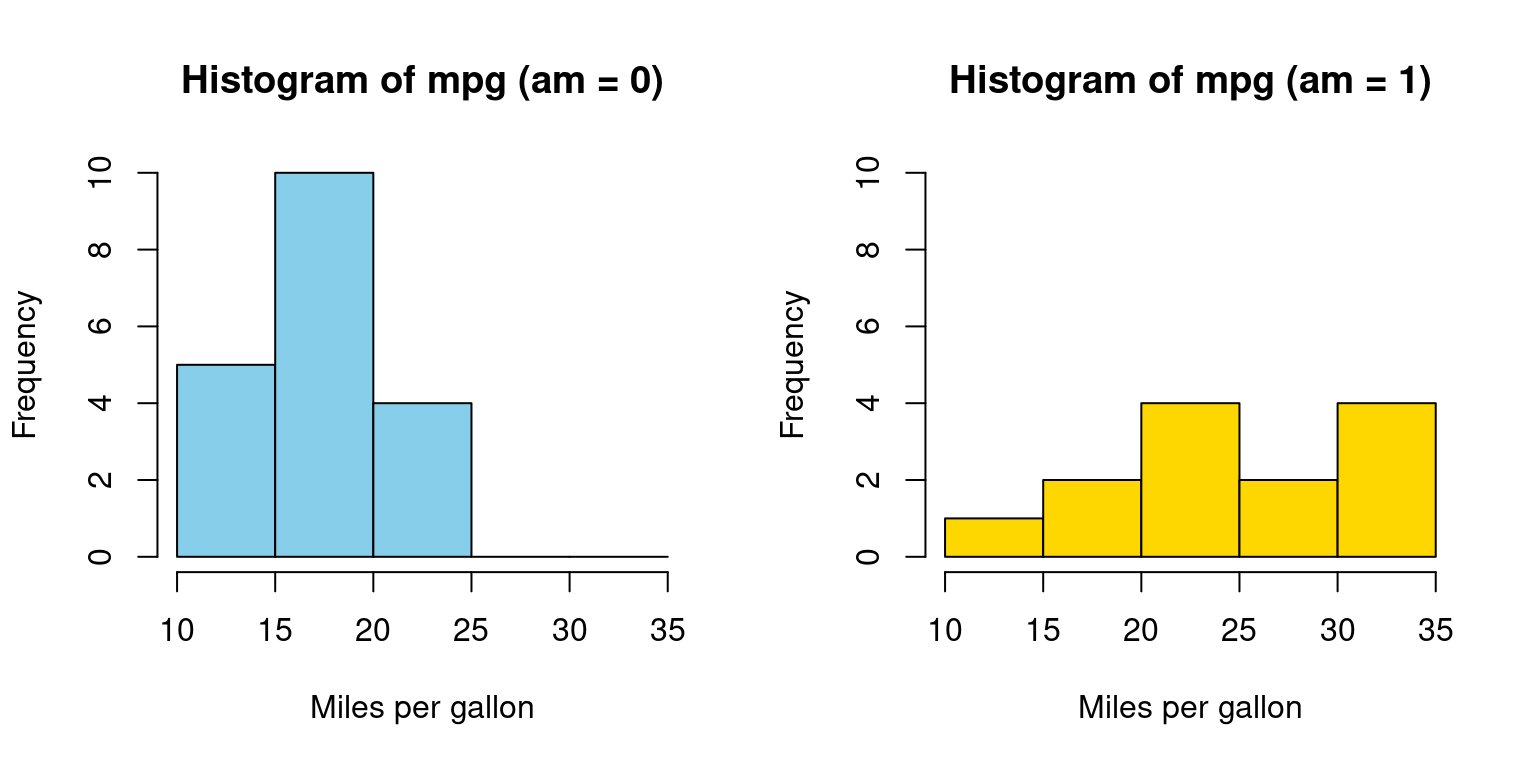

In Appendix A1, we have alternative code written using a for loop

  1. Discussion:

  • We aim to visualize the distribution of the mpg values from the tb dataset based on the am variable, which can be either 0 or 1.

  • Data Splitting: We segregate mpg values into two subsets using the split function, depending on the am values. In R, the double brackets [[ ]] are used to access the elements of a list or a specific column of a data frame. split_data[[1]] accesses the first element of the list split_data.

  • Layout Setting: The par function is configured to display two plots side by side in a single row and two columns format.

  1. Color Vector: We introduce a color_vector to assign distinct colors to each histogram for differentiation.

  2. Histogram: Two histograms are generated, one for each am value (0 and 1). These histograms use various parameters like title, x-axis label, color, and y-axis limits to provide a clear representation of the data’s distribution. [1]

Probability Density Function (PDF) across one Category

  1. Visualizing Probability Density Functions (PDF) of car mileage (mpg) broken down by transmission (am=0,1) [1]
# Splitting 'mpg' data from the 'tb' dataframe by 'am' values.
split_data <- split(tb$mpg, tb$am)

# Setting up the graphical layout for two plots side by side.
par(mfrow = c(1, 2))

# Defining color scheme for the plots.
color_vector <- c("skyblue", "gold")

# Calculating the density for the subset with 'am' equals 0 and plotting it.
dens_0 <- density(split_data[[1]])
plot(dens_0, 
     main = "PDF of mpg for am = 0",  # Title for the first plot.
     xlab = "Miles per gallon",  # X-axis label.
     col = color_vector[1],  # Applying the first color.
     border = "black",
     ylim = c(0, 0.15),  # Setting y-axis limits.
     lwd = 2)  # Line width for the density plot.
polygon(dens_0, col = color_vector[1], border = "black")  
# Filling under the density curve.

# Calculating the density for the subset with 'am' equals 1 and plotting it.
dens_1 <- density(split_data[[2]])
plot(dens_1, 
     main = "PDF of mpg for am = 1",  # Title for the second plot.
     xlab = "Miles per gallon",  # X-axis label.
     col = color_vector[2],  # Applying the second color.
     border = "black",
     ylim = c(0, 0.15),  # Setting y-axis limits.
     lwd = 2)  # Line width for the density plot.
polygon(dens_1, col = color_vector[2], border = "black")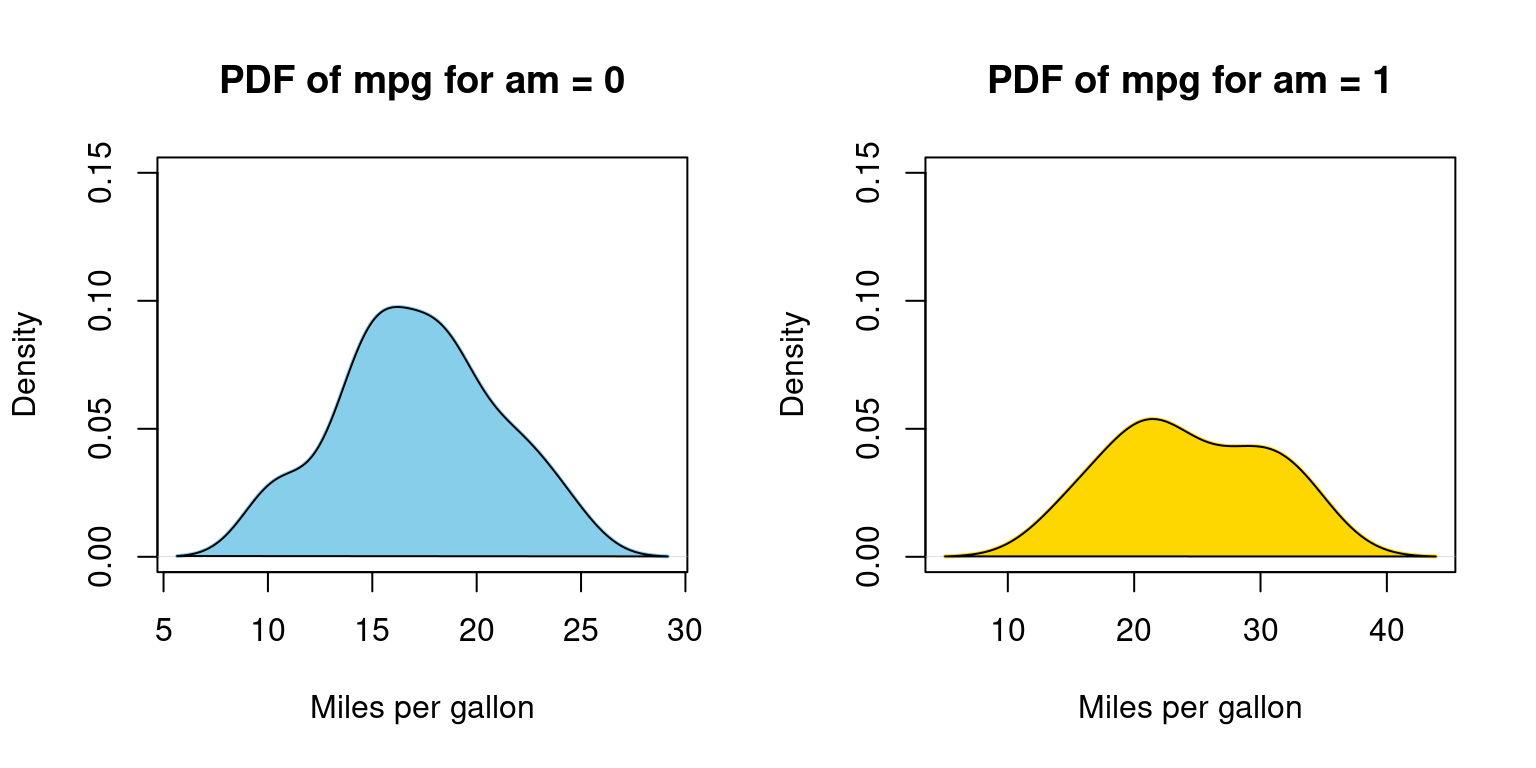  

# Filling under the density curve.

In Appendix A2, we have alternative code written using a for loop

  1. Discussion:

  • dens_0 <- density(split_data[[1]]) calculates the density values for the subset where am is 0.

  • The subsequent plot function visualizes the density curve, setting various parameters like the title, x-axis label, color, and line width.

  • The polygon function fills the area under the density curve with the specified color, giving a shaded appearance to the plot.

  • The process is repeated for the subset where am is 1. The code calculates the density, plots it, and then uses the polygon function to shade the area under the curve. [1]

In Appendix A3, we demonstrate how to draw overlapping PDFs on the same plot, using base R functions.

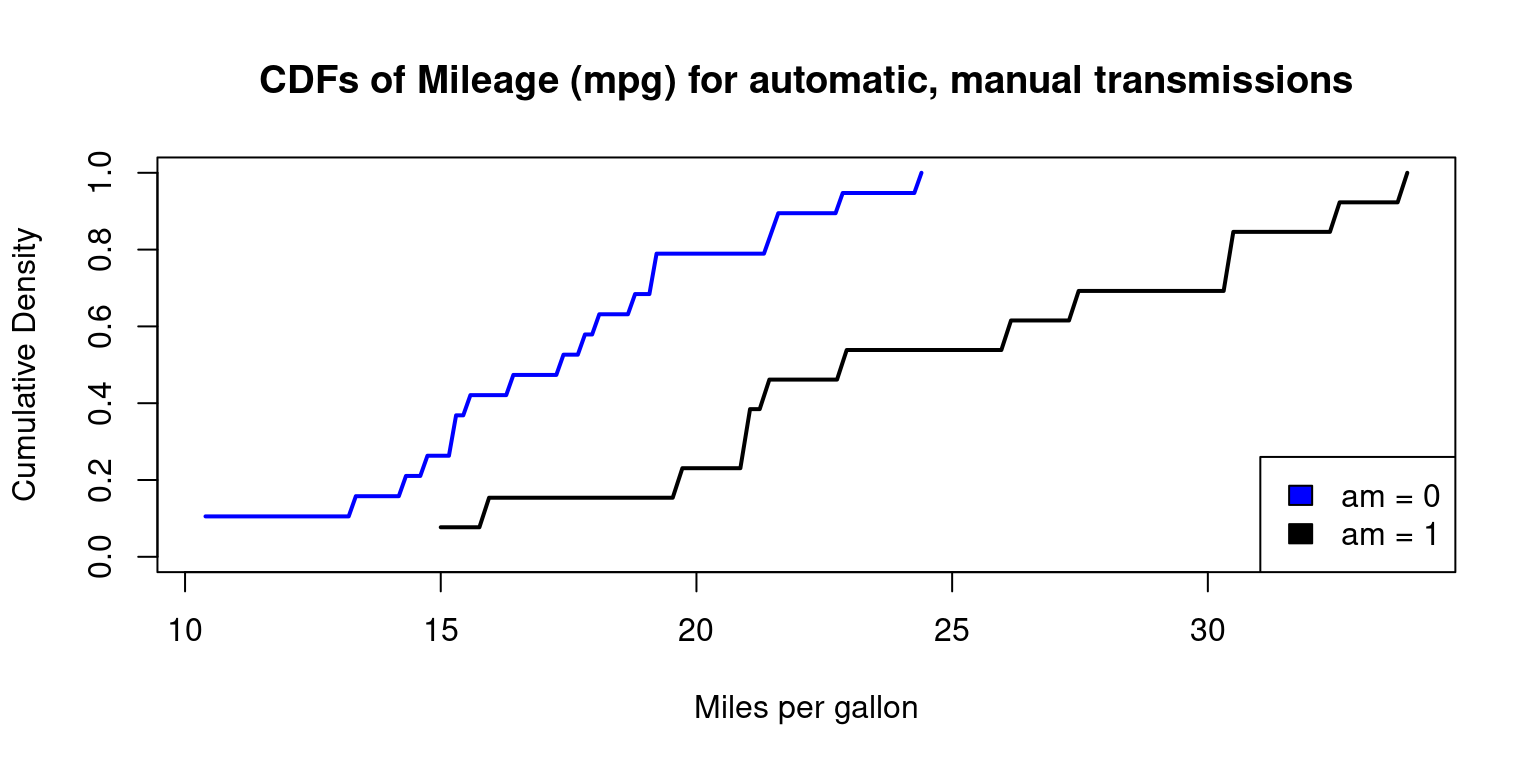
Cumulative Density Function (CDF) across one Category

In Appendix A4, we demonstrate how to draw a CDF, using base R functions

Box Plots across one Category

  1. Visualizing Median using Box Plot – median weight of the cars broken down by cylinders (cyl=4,6,8)
# Creating a boxplot for 'mpg' values grouped by 'cyl'.
boxplot(mpg ~ cyl,
        main = "Boxplot of Mileage (mpg) by Cylinders (cyl=4,6,8)",   
        xlab = "Mileage (mpg)",  # Label for the x-axis.
        ylab = "Cylinders (cyl)",  # Label for the y-axis.
        col = c("skyblue"),  # Color of the boxplots.
        horizontal = TRUE  # Setting the boxplot to be horizontal.
        )

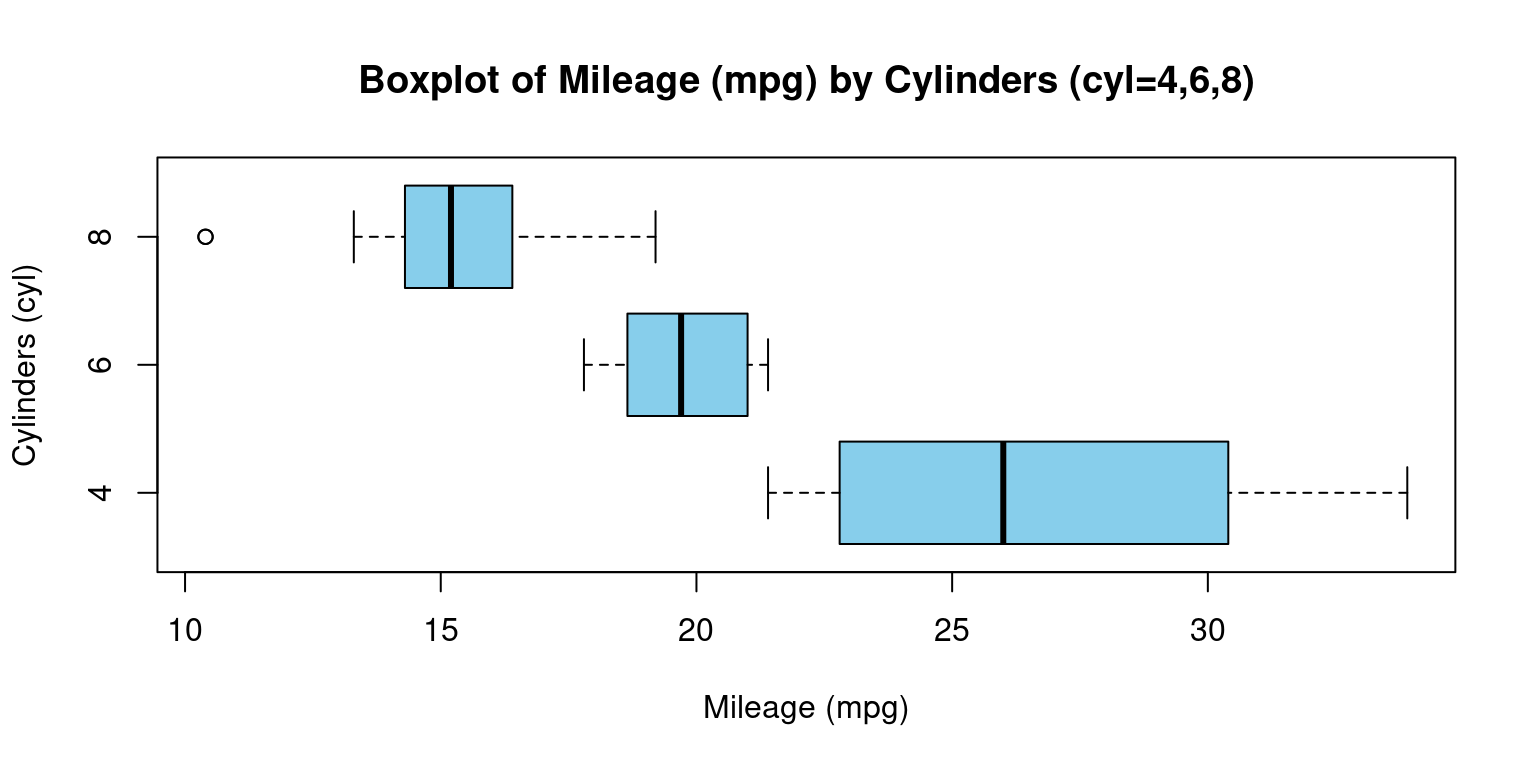
  1. Discussion:

  • This code creates a visual representation of the distribution of miles per gallon (mpg) based on the number of cylinders (cyl), using the boxplot function from the base graphics package in R. down:

  • Data Input: The formula mpg ~ cyl instructs R to create separate boxplots for each unique value of cyl, with each boxplot representing the distribution of mpg values for that particular cylinder count.

  • Title Configuration: main specifies the title of the plot as “Boxplot of Miles Per Gallon (mpg) by Cylinders.”

  • Axis Labels: The labels for the x-axis and y-axis are set using xlab and ylab, respectively. Here, xlab labels the mileage (or mpg), while ylab labels the number of cylinders (cyl).

  • Color Choice: The col argument is set to “skyblue,” which colors the body of the boxplots in a light blue shade.

  • Orientation: By setting horizontal to TRUE, the boxplots are displayed in a horizontal orientation rather than the default vertical orientation.

  • In essence, we’re visualizing the variations in car mileage based on the number of cylinders using horizontal boxplots. This type of visualization helps in understanding the central tendency, spread, and potential outliers of mileage for different cylinder counts.

  1. Visualizing Median using Box Plot – median weight of the cars broken down by cylinders (cyl=4,6,8) and Transmission (am=0,1). [1] [7]
# Creating a boxplot for 'mpg' values grouped by both 'cyl' and 'am'.
boxplot(mpg ~ cyl * am,
        main = "Boxplot of Mileage (mpg) by Cylinders and Transmission",  
        xlab = "Mileage (mpg)",  # Label for the x-axis.
        ylab = "Cylinders & Transmission (cyl:am)",  # Label for the y-axis.
        col = c("skyblue", "gold"), # Colors of the boxplots
        horizontal = TRUE  # Setting the boxplot to be horizontal.
        )

# Adding a legend to the plot.
legend("topright",  # Position of the legend in the plot.
       legend = c("Automatic", "Manual"),  # Text for the legend.
       fill = c("skyblue", "gold"),  # Color filling 
       title = "Transmission"  # Title of the legend.
)

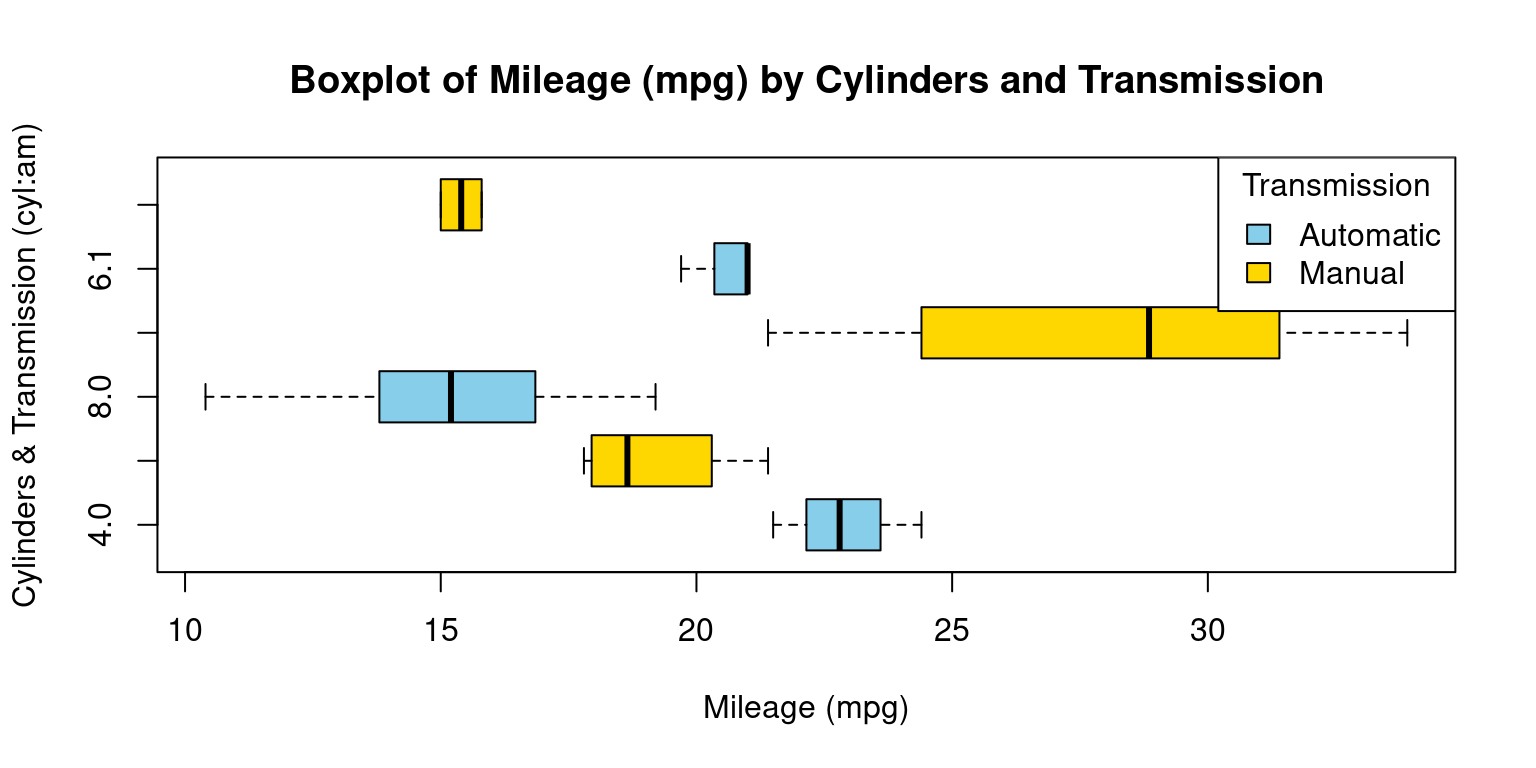
  1. Discussion:

  • This R code presents a horizontal boxplot showcasing the distribution of mileage (mpg) based on the interaction between the number of car cylinders (cyl) and the type of transmission (am).

  • Boxplot Creation: The boxplot function is used to generate the visualization. With the formula mpg ~ cyl * am, we plot the distribution of mpg for every combination of cyl and am.

  • Color Configuration: The col argument specifies the colors for the boxplots. We’ve opted for “skyblue” and “gold” for differentiation. Depending on the order of factor levels in your data, one color typically represents one level of am (e.g., automatic) and the other color represents the second level (e.g., manual).

  • Orientation: The horizontal argument, set to TRUE, orients the boxplots horizontally.

  • Legend Addition: Following the boxplot, we add a legend using the legend function. Placed at the “topright” position, this legend differentiates between “Automatic” and “Manual” transmissions using the designated colors.

  • In essence, our code generates a detailed visualization that elucidates the mileage distribution for various combinations of cylinder counts and transmission types in cars. [7]

Means Plot across one Category

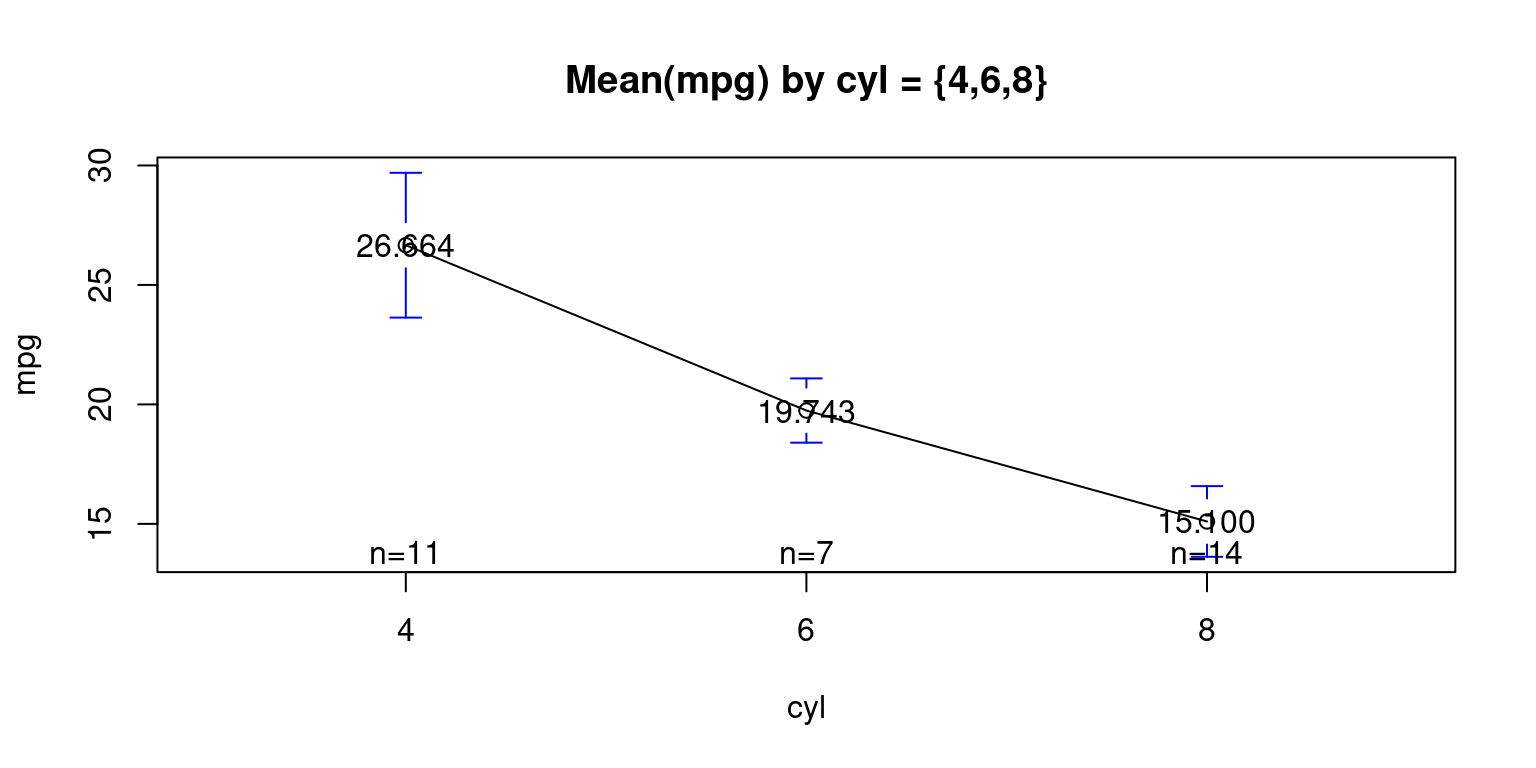
Visualizing Means – mean plot showing the average weight of the cars, broken down by transmission (am= 0 or 1). [8]

# Loading the 'gplots' package
library(gplots)

Attaching package: 'gplots'
The following object is masked from 'package:stats':

    lowess
# Creating a plot of mean 'mpg' values for each 'cyl' category 
plotmeans(data = tb,
          mpg ~ cyl,  # Formula indicating 'mpg' plotted against 'cyl'.
          mean.labels = TRUE,  # Option to display the mean value labels.
          digits = 3,  # Number of digits for the mean value labels.
          main = "Mean(mpg) by cyl = {4,6,8}"  # Main title of the plot.
          )

Means Plot across two Categories

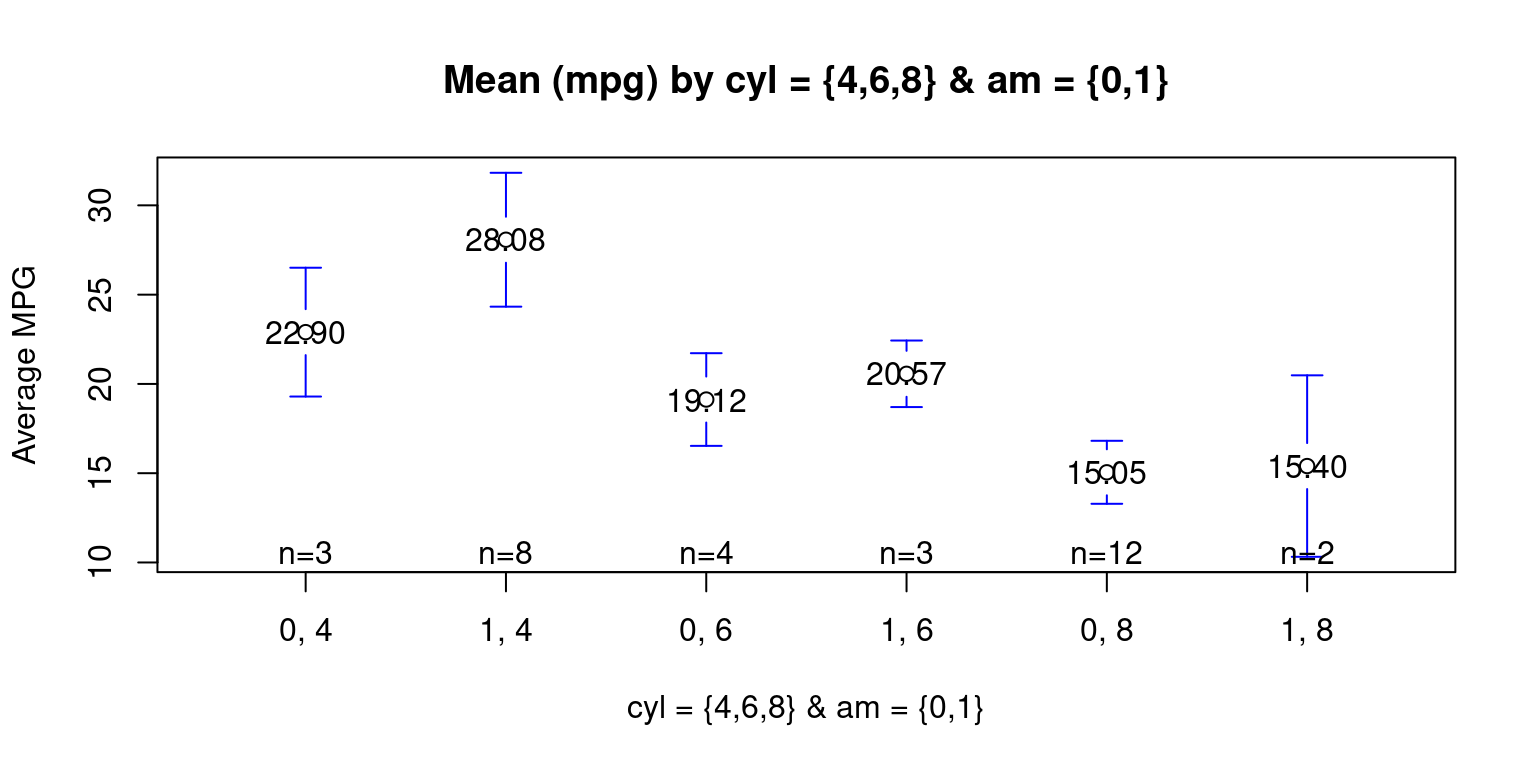
We show a mean plot showing the mean weight of the cars broken down by Transmission Type (am= 0 or 1) & cylinders (cyl = 4,6,8). [8]

# Loading the 'gplots' package for plotting data.
library(gplots)

# The plot will show mean 'mpg' values 
# for each combination of 'am' and 'cyl' categories
plotmeans(mpg ~ interaction(am, cyl, sep = ", "),
          data = tb,  # Specifying the dataframe.
          mean.labels = TRUE,  # display  mean value labels on the plot.
          digits = 2,  # Setting the number of digits to 2.
          connect = FALSE,  # Disabling the connection lines between means.
          main = "Mean (mpg) by cyl = {4,6,8} & am = {0,1}",  
          xlab = "cyl = {4,6,8} & am = {0,1}",  # Label for the x-axis.
          ylab = "Average MPG"  # Label for the y-axis.
          )

Summary of Chapter 12 – Bivariate Continuous data (Part 1 of 4)

This chapter on R programming skillfully navigates the analysis of bivariate continuous data across categorical variables. It begins with preparing the mtcars dataset, transforming key variables like cylinders and transmission type into categorical factors for in-depth analysis.

The chapter primarily focuses on summarizing continuous data using R functions like aggregate(), tapply(), and describeBy() from the psych package. These functions are adept at calculating and presenting summary statistics such as means and standard deviations for different categorical groups.

In terms of visualization, the chapter showcases a variety of methods to graphically represent continuous data across categories. Techniques such as Bee Swarm plots, histograms, density plots, and box plots are highlighted for their effectiveness in illustrating data distributions and variations across categorical groups.

Overall, the chapter provides a comprehensive yet concise framework for analyzing and visualizing the interplay between continuous and categorical data in R, offering valuable insights for data analysis and interpretation.

References

Basic R Programming:

[1] Chambers, J. M. (2008). Software for Data Analysis: Programming with R (Vol. 2, No. 1). Springer.

Crawley, M. J. (2012). The R Book. John Wiley & Sons.

Gardener, M. (2012). Beginning R: The Statistical Programming Language. John Wiley & Sons.

Grolemund, G. (2014). Hands-On Programming with R: Write Your Own Functions and Simulations. O’Reilly Media, Inc.

Kabacoff, R. (2022). R in Action: Data Analysis and Graphics with R and Tidyverse. Simon and Schuster.

Peng, R. D. (2016). R Programming for Data Science (pp. 86-181). Leanpub.

R Core Team. (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/.

Tippmann, S. (2015). Programming Tools: Adventures with R. Nature, 517(7532), 109-110.

Wickham, H., Çetinkaya-Rundel, M., & Grolemund, G. (2023). R for Data Science. O’Reilly Media, Inc.

knitr:

[2] Xie, Y. (2018). knitr: A Comprehensive Tool for Reproducible Research in R. In Implementing Reproducible Research (pp. 3-31). Chapman and Hall/CRC.

psych:

[3] Revelle, W. (2020). psych: Procedures for Psychological, Psychometric, and Personality Research. Northwestern University, Evanston, Illinois. R Package Version 2.0.12. Retrieved from https://CRAN.R-project.org/package=psych.

beeswarm:

[4] Eklund, A. (2020). ggbeeswarm: Categorical Scatter (Violin Point) Plots. R Package Version 0.6.0. Retrieved from https://CRAN.R-project.org/package=ggbeeswarm.

Stem and Leaf:

[5] Lovie, S. (2005). Stem and Leaf Plot. Encyclopedia of Statistics in Behavioral Science.

Histograms:

[6] Scott, D. W. (1979). On Optimal and Data-Based Histograms. Biometrika, 66(3), 605-610.

Wand, M. P., & Jones, M. C. (1995). Kernel Smoothing. Chapman and Hall/CRC.

Box Plots:

[7] McGill, R., Tukey, J. W., & Larsen, W. A. (1978). Variations of Box Plots. The American Statistician, 32(1), 12-16.

gplots:

[8] Warnes, M. G. R., Bolker, B., Bonebakker, L., Gentleman, R., Huber, W., & Liaw, A. (2016). Package ‘gplots’: Various R Programming Tools for Plotting Data.

Statistics using R:

[9] Braun, W. J., & Murdoch, D. J. (2021). A First Course in Statistical Programming with R. Cambridge University Press.

Cohen, Y., & Cohen, J. Y. (2008). Statistics and Data with R: An Applied Approach Through Examples. John Wiley & Sons.

Dalgaard, P. (2008). Introductory Statistics with R. Springer.

Davies, T. M. (2016). The Book of R: A First Course in Programming and Statistics. No Starch Press.

Field, A., Miles, J., & Field, Z. (2012). Discovering Statistics Using R. Sage Publications.

Fox, J., & Weisberg, S. (2018). An R Companion to Applied Regression. Sage Publications.

Hyndman, R. J., & Fan, Y. (1996). Sample Quantiles in Statistical Packages. The American Statistician, 50(4), 361-365.

Matloff, N. (2011). The Art of R Programming: A Tour of Statistical Software Design. No Starch Press.

R Core Team. (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/.

Schumacker, R. E. (2014). Learning Statistics Using R. Sage Publications.

Schumacker, R., & Tomek, S. (2013). Understanding Statistics Using R. Springer Science & Business Media.

Appendix

Appendix A1

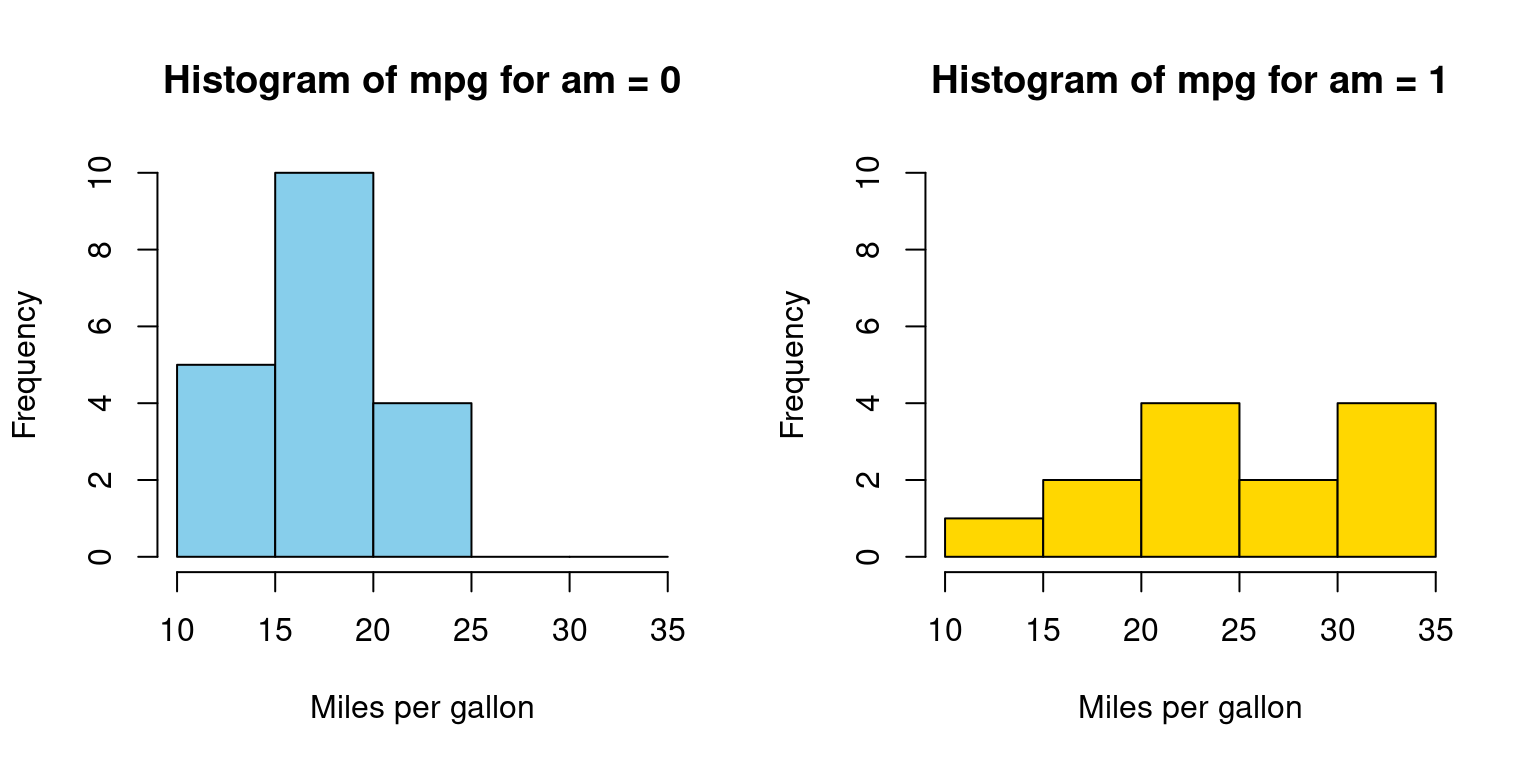
Visualizing histograms of car mileage (mpg) broken down by transmission (am=0,1)

Code written using a for loop

# Split the data by 'am' variable
split_data <- split(tb$mpg, tb$am)

# Create a 1-row 2-column layout
par(mfrow = c(1, 2))

# Define the color vector
color_vector <- c("skyblue", "gold")

# Create a histogram for each subset
for (i in 1:length(split_data)) {
  hist(split_data[[i]], 
       main = paste("Histogram of mpg for am =", i - 1), 
       breaks = seq(10, 35, by = 5), # bins with ranges 10-15, 15-20
       xlab = "Miles per gallon", 
       col = color_vector[i], # Use the color vector, 
       border = "black",
       ylim = c(0, 10))
}

Appendix A2

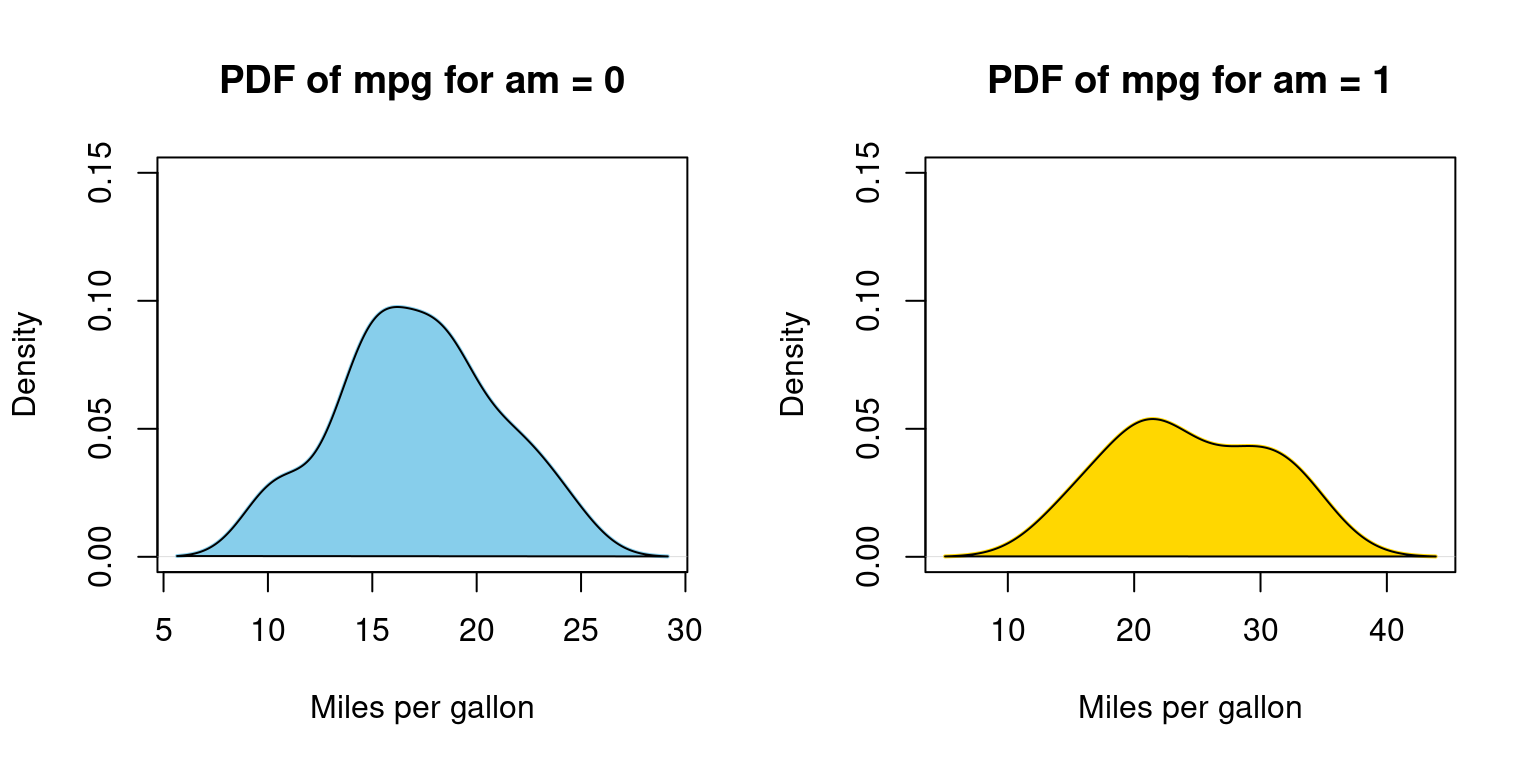
Visualizing Probability Density Function (PDF) of car milegage (mpg) broken down by transmission (am=0,1), using for loop

# Split the data by 'am' variable
split_data <- split(tb$mpg, tb$am)

# Create a 1-row 2-column layout
par(mfrow = c(1, 2))

# Define the color vector
color_vector <- c("skyblue", "gold")

# Create a density plot for each subset
for (i in 1:length(split_data)) {
  # Calculate density
  dens <- density(split_data[[i]])

  # Plot density
  plot(dens, 
       main = paste("PDF of mpg for am =", i - 1), 
       xlab = "Miles per gallon", 
       col = color_vector[i], 
       border = "black",
       ylim = c(0, 0.15), # Adjust this value if necessary
       lwd = 2) # line width

  # Add a polygon to fill under the density curve
  polygon(dens, col = color_vector[i], border = "black")
}

Appendix A3

Visualizing Probability Density Function (PDF) of car milegage (mpg) broken down by transmission (am=0,1), overlapping PDFs on the same plot

# Split the data by 'am' variable
split_data <- split(tb$mpg, tb$am)

# Define the color vector
color_vector <- c("skyblue", "gold")

# Define the legend labels
legend_labels <- c("am = 0", "am = 1")

# Create a density plot for each subset
# Start with an empty plot with ranges accommodating both data sets
plot(0, 0, 
     xlim = range(tb$mpg), ylim = c(0, 0.15), 
     type = "n", 
     xlab = "Miles per gallon", ylab = "Density", 
     main = "PDFs of mpg for automatic, manual transmissions")

for (i in 1:length(split_data)) {
  # Calculate density
  dens <- density(split_data[[i]])
  
  # Add density plot
  lines(dens, 
        col = color_vector[i], 
        lwd = 2) # line width

  # Add a polygon to fill under the density curve
  polygon(dens, 
          col = adjustcolor(color_vector[i], 
                            alpha.f = 0.8), 
          border = "black")
}

# Add legend to the plot
legend("topright", 
       legend = legend_labels, 
       fill = color_vector, 
       border = "black")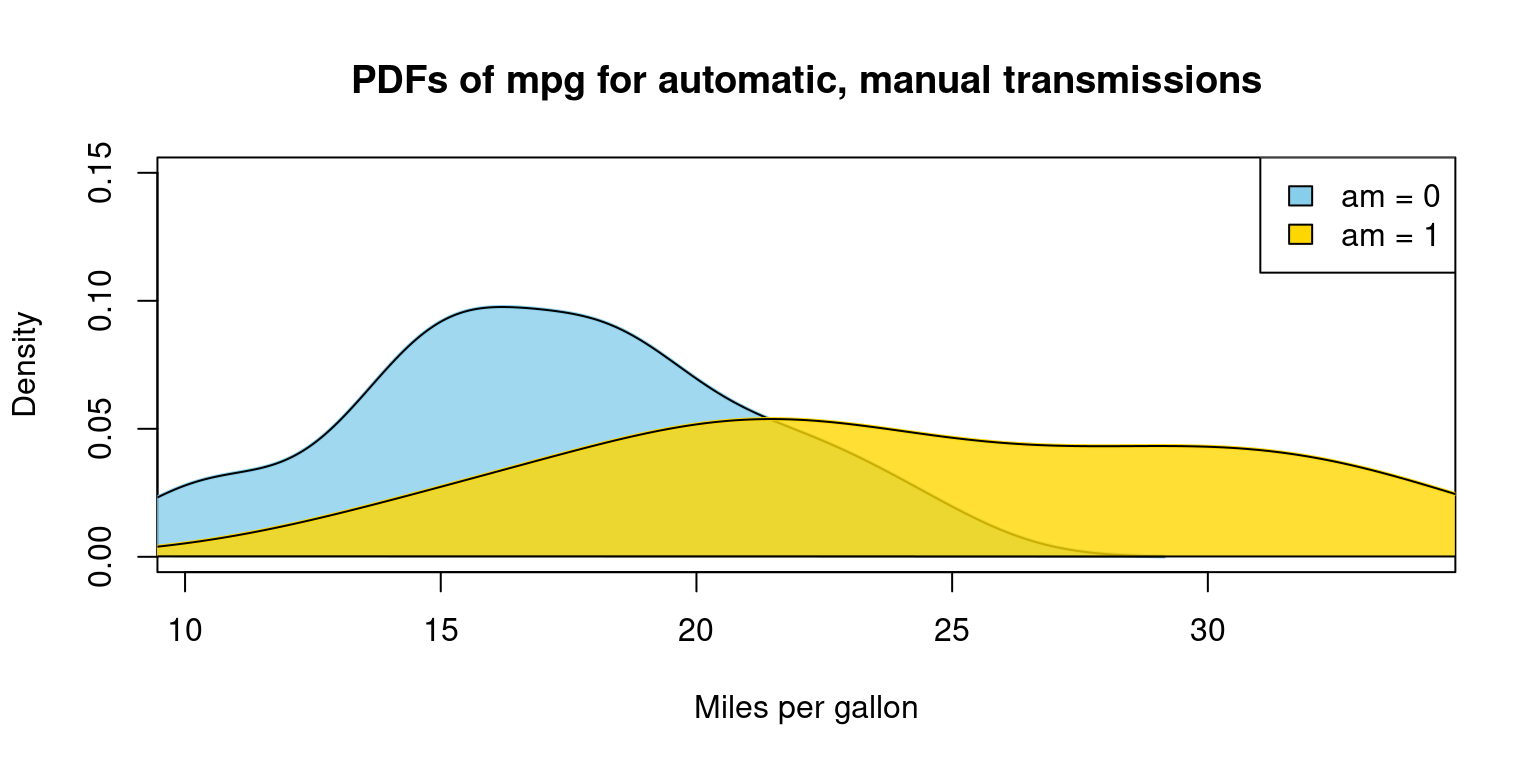

Appendix A4

# Split the data by 'am' variable
split_data <- split(tb$mpg, tb$am)

# Define the color vector
color_vector <- c("blue", "black")

# Define the legend labels
legend_labels <- c("am = 0", "am = 1")

# Create a cumulative density plot for each subset
# Start with an empty plot with ranges accommodating both data sets
plot(0, 0, xlim = range(mtcars$mpg), ylim = c(0, 1), type = "n", 
     xlab = "Miles per gallon", ylab = "Cumulative Density", 
     main = "CDFs of Mileage (mpg) for automatic, manual transmissions")

for (i in 1:length(split_data)) {
  # Calculate empirical cumulative density function
  ecdf_func <- ecdf(split_data[[i]])
  
  # Add CDF plot using curve function
  curve(ecdf_func(x), 
        from = min(split_data[[i]]), to = max(split_data[[i]]), 
        col = color_vector[i], 
        add = TRUE, 
        lwd = 2) # line width
}
# Add legend to the plot
legend("bottomright", 
       legend = legend_labels, 
       fill = color_vector, 
       border = "black")