Univariate Continuous data (Part 1 of 2)

Chapter 10.

Exploring Univariate Continuous Data

This chapter explores how to summarize and visualize univariate, continuous data.

  1. Univariate continuous data refers to data coming from one feature or variable, which could take on an infinite number of possible values, typically within an interval [1].

  2. For instance, in the mtcars dataset in R, variables like mpg (miles per gallon), wt (weight), and hp (horsepower) epitomize continuous data. They are not limited to specific, separate numbers and can encompass any value, including decimal points, within their respective ranges.

  3. Data: Suppose we run the following code to prepare the mtcars data for subsequent analysis and save it in a tibble called tb. [1]

# Load the required libraries, suppressing annoying startup messages
library(dplyr, quietly = TRUE, warn.conflicts = FALSE)
library(tibble, quietly = TRUE, warn.conflicts = FALSE)

# Read the mtcars dataset into a tibble called tb
data(mtcars)
tb <- as_tibble(mtcars)

# Convert relevant columns into factor variables
tb$cyl <- as.factor(tb$cyl) # cyl = {4,6,8}, number of cylinders
tb$am <- as.factor(tb$am) # am = {0,1}, 0:automatic, 1: manual transmission
tb$vs <- as.factor(tb$vs) # vs = {0,1}, v-shaped engine, 0:no, 1:yes
tb$gear <- as.factor(tb$gear) # gear = {3,4,5}, number of gears

# Directly access the data columns of tb, without tb$mpg
attach(tb)

Measures of Central Tendency

  1. In our journey of understanding data, we often turn to certain statistical tools, among which, the measures of central tendency play a pivotal role. These measures provide a way to summarize our data with a single value that represents the “center” or the “average” of our data distribution. [2]

  2. Primarily, there are three measures of central tendency that we often rely on: the mean, median, and mode. [2]

  3. As an illustration, here is R code to determine the mean and median of the wt (weight) for all vehicles: [3]

# Mean of wt
mean(wt)
[1] 3.21725
# Median of wt
median(wt)
[1] 3.325

Measures of Variability

  1. In our exploration of continuous data, we also consider measures of variability. These statistical measures provide insight into the spread or dispersion of our data points. To further illustrate the concepts we’ve discussed, we’ll apply these measures of variability to the mpg column from the mtcars dataset. [3]

  2. Range: This is the difference between the highest and the lowest value in our data set. However, while range is easy to calculate and understand, it is sensitive to outliers, so we must interpret it carefully. The range() function in R provides the minimum and maximum mpg. [3]

# Range of mpg
range(mpg)
[1] 10.4 33.9
  1. Min and Max: We can off course measure the minimum and maximum values, using the following simple code. [3]
# Minimum mpg
min(mpg)
[1] 10.4
# Maximum mpg
max(tb$mpg)
[1] 33.9
  1. Variance: It is calculated as the average of the squared deviations from the mean. Larger variances suggest that the data points are more spread out around the mean. One limitation of the variance is that its units are the square of the original data’s units, which can make interpretation difficult. We use the var() function to compute the variance. [3]
# Variance of mpg
var(tb$mpg)
[1] 36.3241
  1. Standard Deviation: This is simply the square root of the variance. Because it is in the same units as the original data, it is often easier to interpret than the variance. A larger standard deviation indicates a greater spread of data around the mean. [3]
# Standard Deviation of mpg
sd(tb$mpg)
[1] 6.026948
  1. Interquartile Range (IQR): It is another measure of dispersion, especially useful when we have skewed data or outliers. It represents the range within which the central 50% of our data falls. This measure is less sensitive to extreme values than the range, variance, or standard deviation. To find the interquartile range (IQR), which provides the spread of the middle 50% of the mpg values, we use the IQR() function. [3]
# Inter-Quartile Range of mpg
IQR(tb$mpg)
[1] 7.375
  1. Skewness and Kurtosis:

  • Skewness is a measure of the asymmetry of our data. Positive skewness indicates a distribution with a long right tail, while negative skewness indicates a distribution with a long left tail.

  • Kurtosis, on the other hand, measures the “tailedness” of the distribution. A distribution with high kurtosis exhibits a distinct peak and heavy tails, while low kurtosis corresponds to a flatter shape.

  • These two measures can be computed using the skewness() and kurtosis() functions from the moments package.

# Load moments package
suppressPackageStartupMessages(library(moments))

# Skewness of 'wt' in the mtcars dataframe
skewness(tb$wt)
[1] 0.4437855
# Kurtosis of 'wt' in the mtcars dataframe
kurtosis(tb$wt)
[1] 3.172471
  1. Overall, these measures of variability help us quantify the dispersion and shape of our data, offering a more complete picture when combined with measures of central tendency. [3]

Summarizing Univariate Continuous Data

  1. Our primary objective in summarizing data is to gain an initial overview or snapshot of the data set we’re dealing with. This fundamental analysis provides us a sense of the data’s central tendency, spread, and distribution shape, which in turn guides our decision-making process for subsequent stages of data analysis.

  2. In R, the summary() function offers a succinct summary of the selected data object. When applied to a numeric vector such as mpg from the mtcars dataset, it yields the minimum and maximum values, the first quartile (25th percentile), the median (50th percentile), the third quartile (75th percentile), and the mean. [3]

# A summary of 'mpg'
summary(tb$mpg)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  10.40   15.43   19.20   20.09   22.80   33.90
  1. The describe() function, part of the psych package, goes a step further by providing a more comprehensive summary of the data. It includes additional statistics like the number of valid (non-missing) observations, the standard deviation, and metrics of skewness and kurtosis [4].
suppressPackageStartupMessages(library(psych))

# A summary of 'mpg' using describe()
describe(mpg)
   vars  n  mean   sd median trimmed  mad  min  max range skew kurtosis   se
X1    1 32 20.09 6.03   19.2    19.7 5.41 10.4 33.9  23.5 0.61    -0.37 1.07
  1. Specific columns from describe(tb$mpg)
# Select specific columns from describe(mpg)
columns = c("n","mean","sd","median","min","max","skew","kurtosis")
describe(mpg)[, columns]
    n  mean   sd median  min  max skew kurtosis
X1 32 20.09 6.03   19.2 10.4 33.9 0.61    -0.37

Summarizing an entire dataframe or tibble

  1. The function summary() in R can also be employed to summarize the entirety of a dataframe or tibble in a comprehensive manner. [3].
# A summary of the tibble tb
summary(tb)
      mpg        cyl         disp             hp             drat      
 Min.   :10.40   4:11   Min.   : 71.1   Min.   : 52.0   Min.   :2.760  
 1st Qu.:15.43   6: 7   1st Qu.:120.8   1st Qu.: 96.5   1st Qu.:3.080  
 Median :19.20   8:14   Median :196.3   Median :123.0   Median :3.695  
 Mean   :20.09          Mean   :230.7   Mean   :146.7   Mean   :3.597  
 3rd Qu.:22.80          3rd Qu.:326.0   3rd Qu.:180.0   3rd Qu.:3.920  
 Max.   :33.90          Max.   :472.0   Max.   :335.0   Max.   :4.930  
       wt             qsec       vs     am     gear        carb      
 Min.   :1.513   Min.   :14.50   0:18   0:19   3:15   Min.   :1.000  
 1st Qu.:2.581   1st Qu.:16.89   1:14   1:13   4:12   1st Qu.:2.000  
 Median :3.325   Median :17.71                 5: 5   Median :2.000  
 Mean   :3.217   Mean   :17.85                        Mean   :2.812  
 3rd Qu.:3.610   3rd Qu.:18.90                        3rd Qu.:4.000  
 Max.   :5.424   Max.   :22.90                        Max.   :8.000
  1. Discussion

  • For numeric columns, summary() delivers a six-number summary that includes minimum, first quartile (Q1 or 25th percentile), median (Q2 or 50th percentile), mean, third quartile (Q3 or 75th percentile), and maximum. This gives a broad understanding of the central tendency and dispersion of the data within each numeric column.

  • For categorical (factor) columns, summary() generates the counts of each category level. The output of this code is essentially a comprehensive snapshot of the tb tibble, enabling us to quickly understand the nature of our data. [3]

  1. To obtain a more detailed statistical summary of an entire dataframe or tibble, we can employ the describe() function from the psych package [4].
# Select specific columns from describe(mpg)
columns = c("n","mean","sd","median","min","max","skew","kurtosis")
describe(tb)[, columns]
       n   mean     sd median   min    max  skew kurtosis
mpg   32  20.09   6.03  19.20 10.40  33.90  0.61    -0.37
cyl*  32   2.09   0.89   2.00  1.00   3.00 -0.17    -1.76
disp  32 230.72 123.94 196.30 71.10 472.00  0.38    -1.21
hp    32 146.69  68.56 123.00 52.00 335.00  0.73    -0.14
drat  32   3.60   0.53   3.70  2.76   4.93  0.27    -0.71
wt    32   3.22   0.98   3.33  1.51   5.42  0.42    -0.02
qsec  32  17.85   1.79  17.71 14.50  22.90  0.37     0.34
vs*   32   1.44   0.50   1.00  1.00   2.00  0.24    -2.00
am*   32   1.41   0.50   1.00  1.00   2.00  0.36    -1.92
gear* 32   1.69   0.74   2.00  1.00   3.00  0.53    -1.07
carb  32   2.81   1.62   2.00  1.00   8.00  1.05     1.26
  1. Discussion:

  • The describe() function analyzes each column in the provided tibble individually and outputs a range of useful statistics. For numeric columns, it offers count, mean, standard deviation, trimmed mean, minimum and maximum values, range, skewness, and kurtosis among others.

  • For non-numeric or factor columns, the describe() function still provides a count of elements but defaults to NA for the rest of the statistics, as these metrics are not applicable.

Visualizing Univariate Continuous Data

  • In our journey to explore and understand univariate continuous data, visualizations act as our valuable companions. Visual graphics provide us with an instant and clear understanding of the underlying data patterns and distributions that may otherwise be challenging to discern from raw numerical data.

  • Let’s take a closer look at some of the most effective ways of visualizing univariate continuous data, including

  1. Bee Swarm plots;

  2. Stem-and-Leaf plots

  3. Histograms;

  4. PDF and CDF Density plots;

  5. Box plots;

  6. Violin plots;

  7. Quantile-Quantile (Q-Q) Plots

Bee Swarm Plot

  1. A Bee Swarm plot is a one-dimensional scatter plot that reduces overlap and provides a better representation of the distribution of individual data points. This type of plot provides a more detailed view of the data, particularly for smaller data sets. [5]
# Load the beeswarm package
library(beeswarm)

# Create a bee swarm plot of wt column
beeswarm(tb$wt, 
         main="Bee Swarm Plot of Weight (wt)", 
         xlab = "Weight ('000 kg)",
         pch=16,  # type of points
         cex=0.8, # size of the points
         col="blue",
         horizontal = TRUE)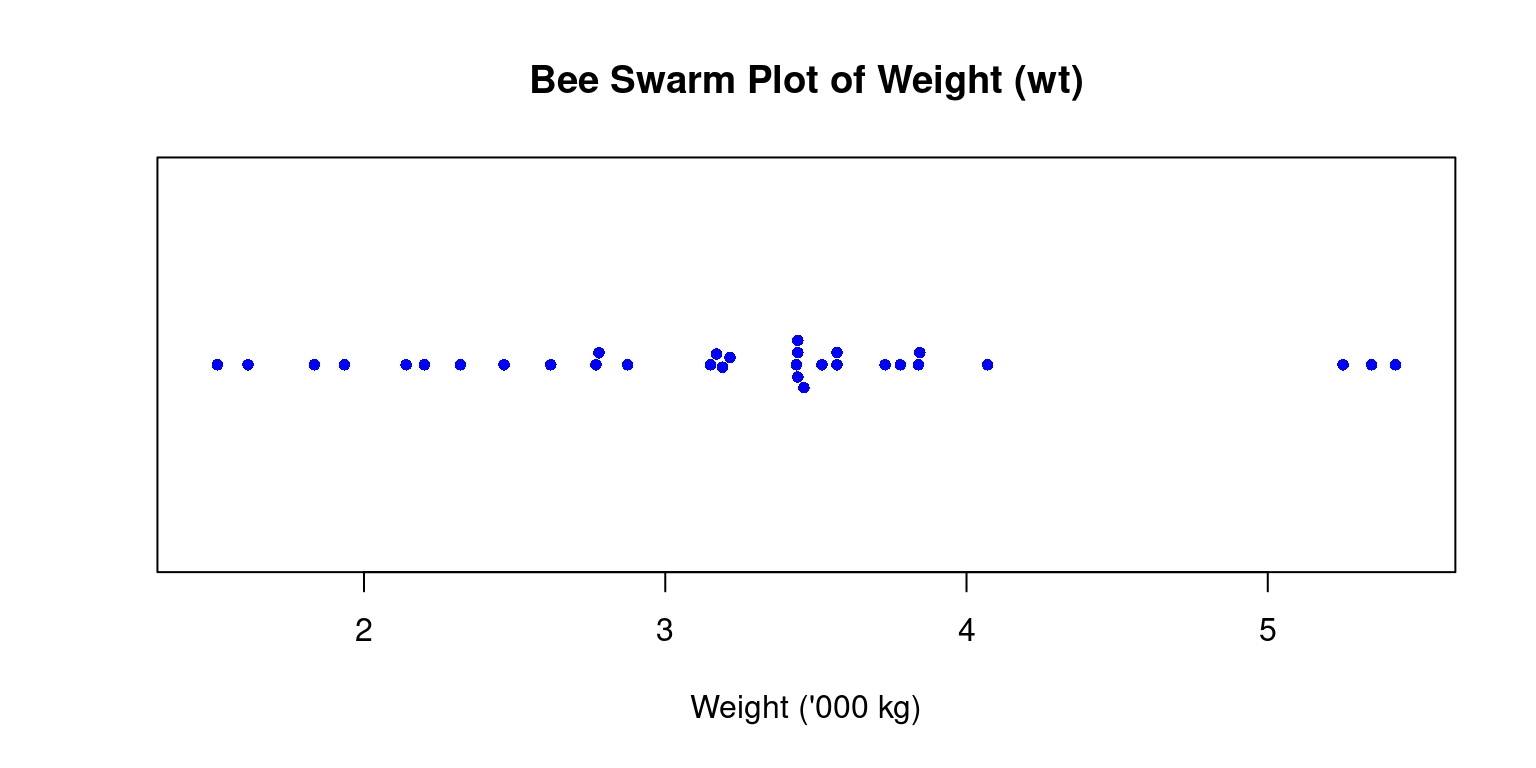

  1. Discussion

  • In the above code, we load the beeswarm package using the library() function.

  • We then create a bee swarm plot of the wt column using the beeswarm() function.

  • The main argument is used to specify the title of the plot.

  • The pch argument is used to set the type of points to be plotted, and the cex argument is used to set the size of the points.

  • The col argument is used to set the color of the points.

  • The resulting plot displays the individual wt values in the dataset as points on a horizontal axis, with no overlap between points. This provides a visual representation of the distribution of the data, as well as any outliers or gaps in the data.

  • horizontal = TRUE: Renders it horizontally rather than the default vertical orientation.

Stem-and-Leaf Plot

  1. Stem-and-leaf plots serve as an efficient tool for visualizing the distribution of data, particularly when working with small to medium-sized datasets. The method involves breaking down each data point into a “stem” and a “leaf”, with the “stem” representing the primary digit(s) and the “leaf” embodying the subsequent digit(s) [7]

  2. We can utilize the stem() function in R to devise stem-and-leaf plots. Here’s how we can apply it to the wt column:

stem(wt)

  The decimal point is at the |

  1 | 5689
  2 | 123
  2 | 56889
  3 | 22224444
  3 | 55667888
  4 | 1
  4 | 
  5 | 334

  1. In the resulting plot, the vertical bar (“|”) symbolizes the decimal point’s location.

  2. This visual representation enables us to swiftly assess the data’s distribution, the center, and the spread, in a fashion similar to a histogram. However, unlike a histogram, a stem-and-leaf plot retains the original data to a certain degree, providing more granular detail.

Histogram

  1. A histogram is a graphical representation showcasing the frequency of discrete or grouped data points within a dataset.

  2. It splits the data into equal-width bins, with the height of each bar matching the frequency of data points in each respective bin.

  3. It serves as a valuable tool for demonstrating the distribution shape of the data. In R, we can construct a histogram using the hist() function and control its appearance. The final histogram visually depicts the frequency of mpg values in the dataset, where each bar represents the count of observations within a specific range of values. [6]

# Create a histogram of mpg column with bins of equal width
hist(tb$mpg, 
     breaks = 12, # This creates 12 bins of equal width
     main="Histogram of mpg (with 12 breaks)", 
     xlab="Miles per gallon (mpg", 
     col="lightblue", 
     border="black")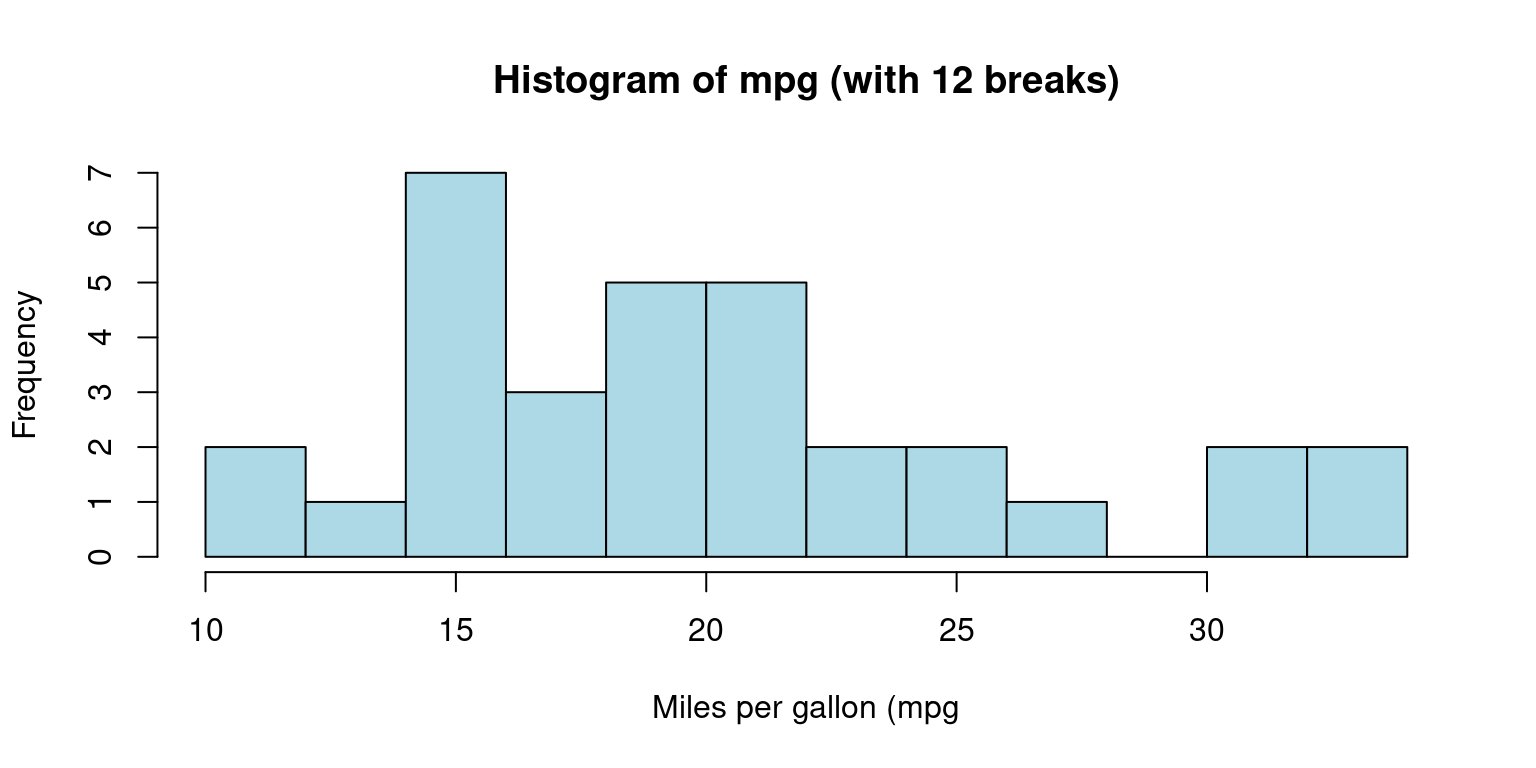

  1. Discussion:

  • This code generates a histogram of mpg using the hist() function. The main argument denotes the plot’s title, while the xlab argument labels the x-axis.

  • We use the col argument to specify the color of the histogram bars, and the border argument to determine the color of the bar borders.

  • We can control the number of bins or the ranges of the bins in a histogram using the breaks argument inside the hist() function:

  1. We can alternately specify the ranges of the bins:
# Create a histogram of mpg column with specific bin ranges
hist(tb$mpg, 
     breaks = seq(5, 35, by = 5), # bins with ranges 10-15, 15-20, etc.
     main="Histogram of Mileage (with breaks of 5)", 
     xlab="Miles per gallon (mpg)", 
     col="lightblue", 
     border="black")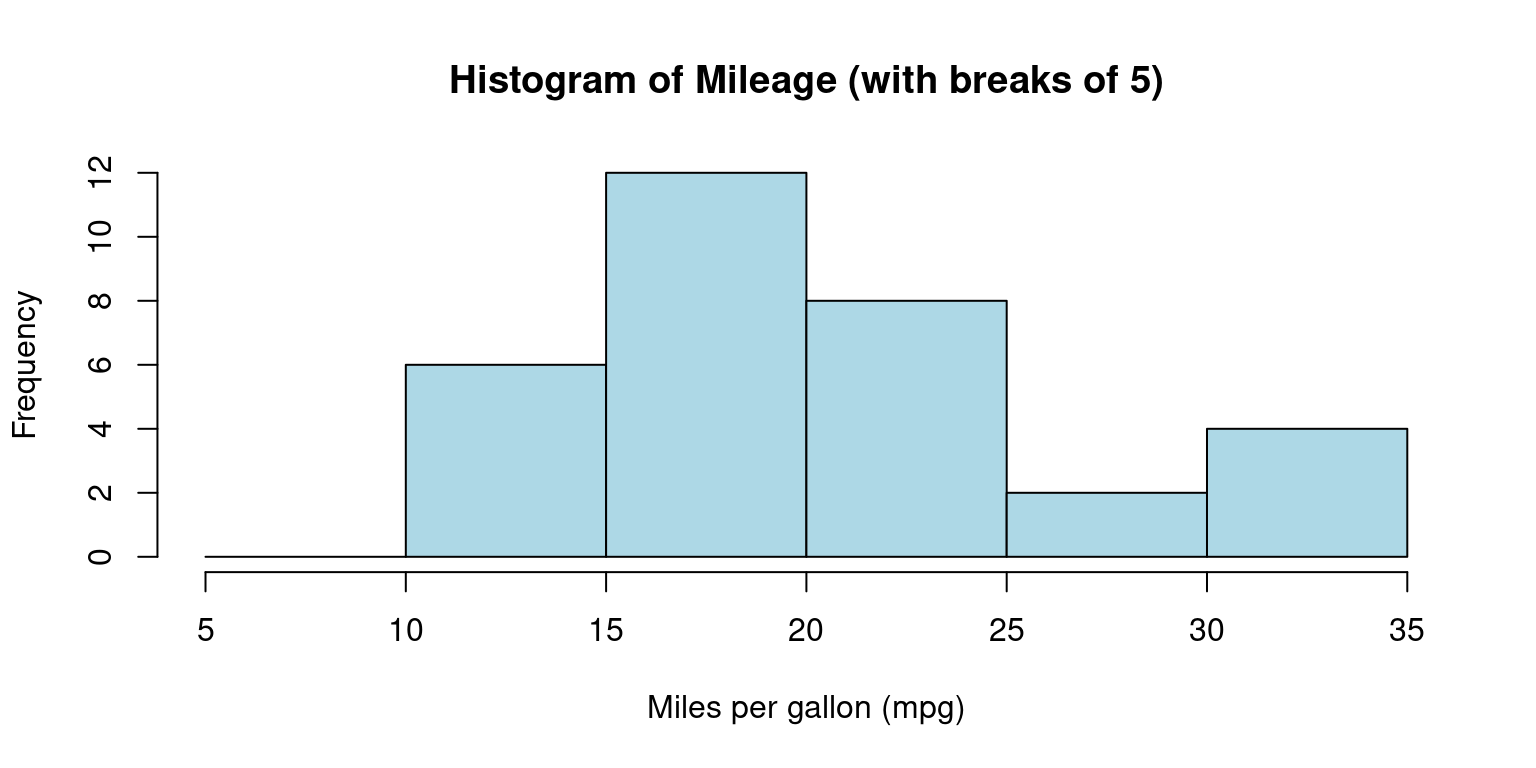

  1. Discussion:

  • The breaks argument uses the seq() function to create a sequence of break points from 5 to 35, with a step of 5.

  • This results in bins with ranges 5-10, 10-15, 15-20, 20-25, 25-30, and 30-35. [7]

Probability Density Function (PDF) plot

  1. Smoothed approximations of histograms are often represented by density plots, as they assist in offering an estimation of the underlying continuous probability distribution of a given dataset. [3]

  2. Compared to histograms, these plots often present superior accuracy and aesthetic appeal, and they eliminate the need for arbitrary bin selection. A density plot shares several similarities with a histogram. However, instead of presenting the frequency of individual values, it conveys the probability density of the dataset. [3]

# Calculate density
dens <- density(mtcars$mpg)
# Create a density plot
plot(dens, 
     main = "Probability Density Function (PDF) of Mileage (mpg)", 
     xlab = "Miles per gallon (mpg)", 
)
# Add a polygon to fill under the density curve
polygon(dens, col = "lightblue", border = "black")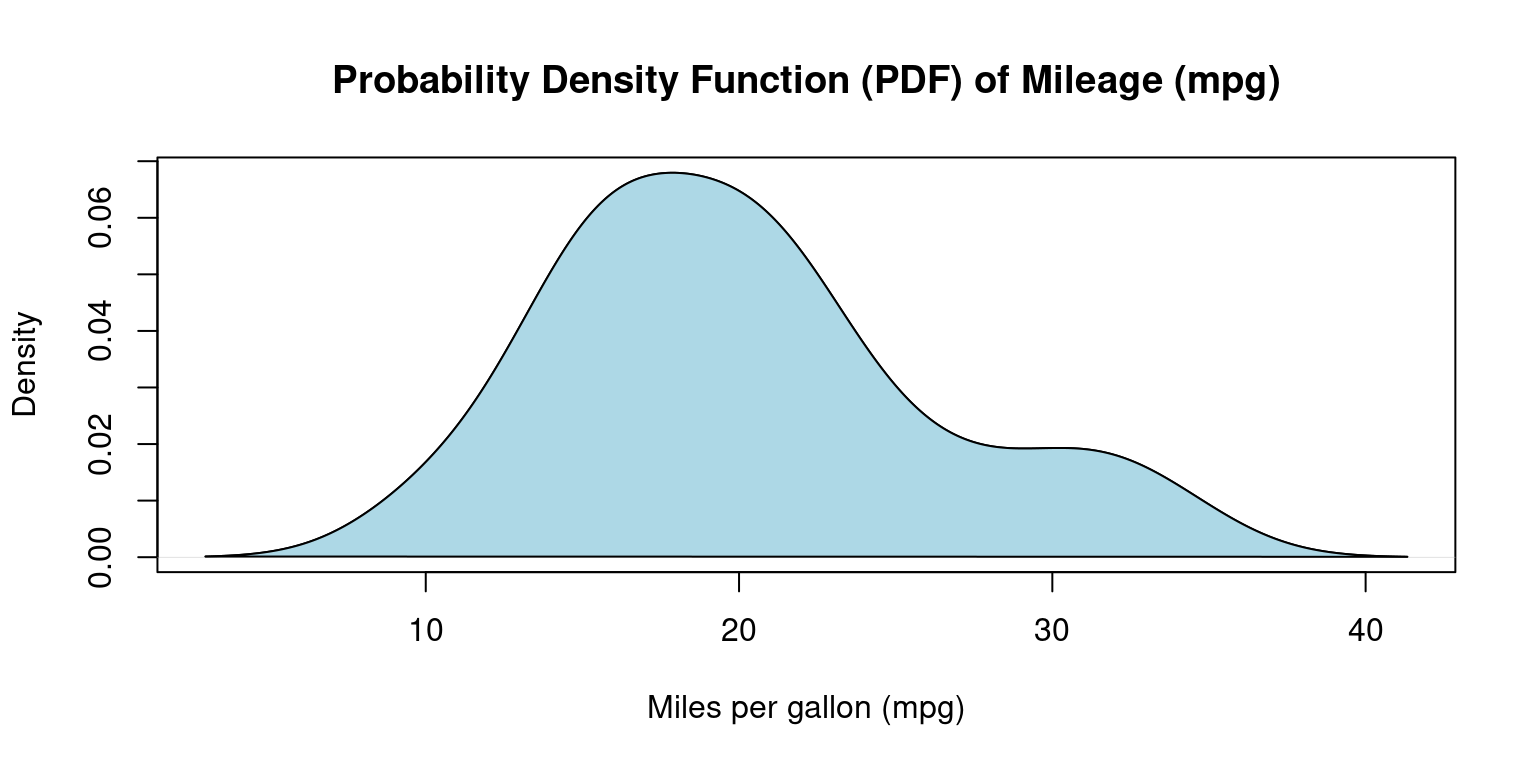

  1. Discussion:

  • We use the density() function to generate a PDF plot for the mpg column.

  • Here, we utilize the plot() function to graph the resulting density object.

  • The main argument stipulates the title of the plot, while the xlab argument designates the label for the x-axis.

  • Through the polygon() function, we determine the shaded color.

  • The final plot displays the probability density of mpg values, using the curve to signify the data distribution. [3]

Cumulative Distribution Function (CDF) Plot

  1. CDF plots visualize the fraction of data points that are less than or equal to a specified value on the x-axis [3].

  2. They facilitate easy representation of the median, percentiles, and spread.

  3. In R, we can employ the ecdf() function to generate a CDF plot.

# Create a CDF plot of mpg column
plot(ecdf(tb$mpg),
     main = "CDF of Miles Per Gallon (mpg)",
     xlab = "Miles Per Gallon (mpg)",
     ylab = "Cumulative Density",
     col = "blue",       # Line color
     lty = 2,
     )
grid(col = "gray", lty = "dotted")  # Add a grid to the plot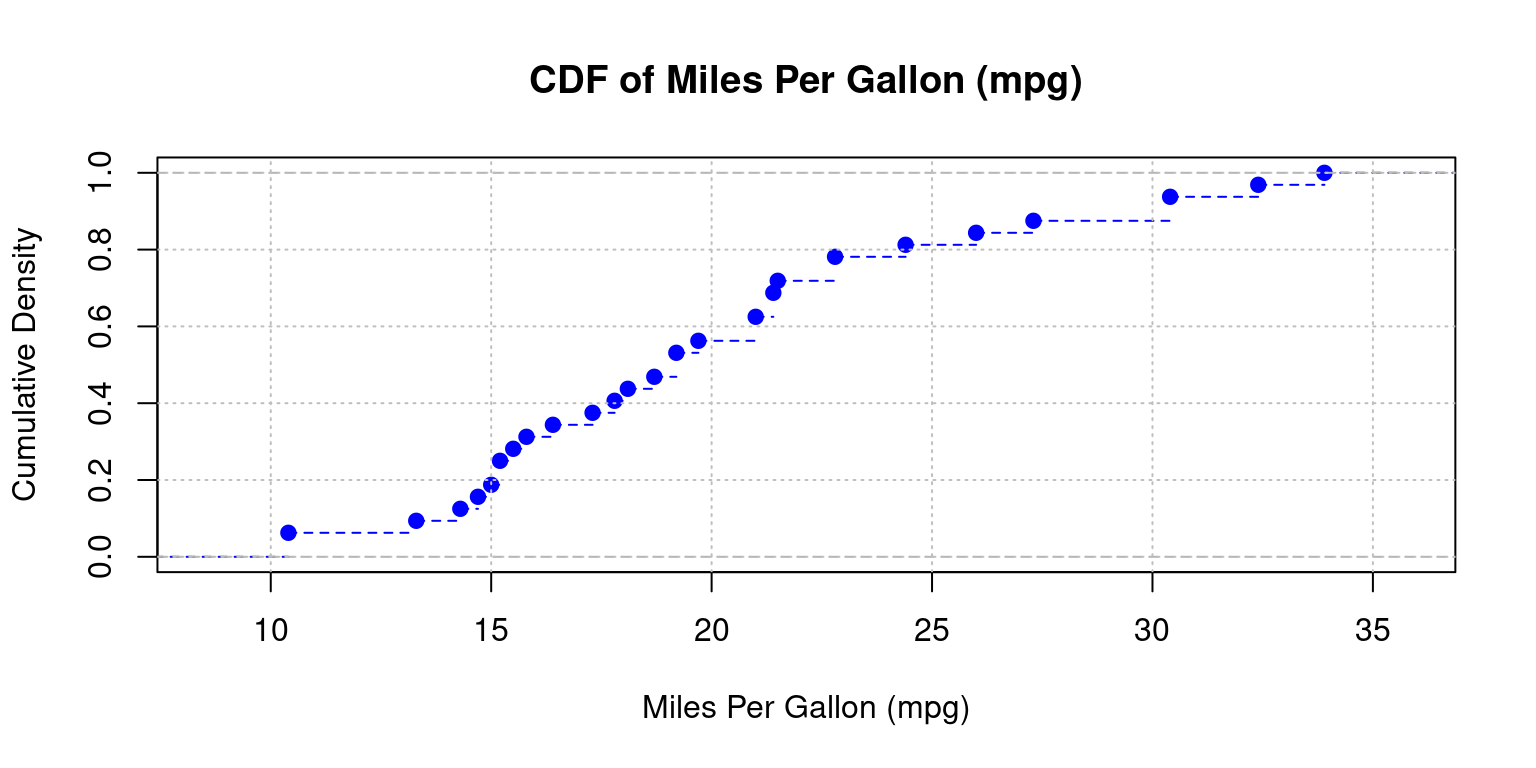

  1. Discussion:

  • ecdf(tb$mpg): The function ecdf() computes the empirical cumulative distribution function (CDF) for the mpg column from the tb data frame.

  • plot(ecdf(tb$mpg)): Plots the CDF of the mpg column.

  • main, xlab, ylab: Set the title and axis labels.

  • col = "blue": Colors the plot line blue; lty = 2: Uses a dashed line.

  • grid(col = "gray", lty = "dotted"): Adds a gray, dotted grid to the plot.

  1. Computing and Inversing CDF Values

  • The following code demonstrates how to determine the cumulative distribution function (CDF) value for a given mpg using ecdf() and how to find the mpg value corresponding to a specific CDF with quantile().

  • Suppose we want to identify the CDF at mpg = 20, here is how we do it:

# Generate the empirical cumulative distribution function
ecdf_func <- ecdf(tb$mpg)

# Derive the CDF for mpg = 20
ecdf_func(20)
[1] 0.5625
  • If we’re interested in knowing the mpg value that corresponds to a certain CDF value, the quantile() function comes to our aid. For instance, we can obtain the mpg value associated with a CDF of 0.6 as follows:
# Discover the mpg corresponding to CDF = 0.6
quantile(tb$mpg, 0.6)
60% 
 21

Box Plot

  1. Box-and-whisker plots, commonly known as box plots, are crucial graphical instruments for illustrating a distribution’s center, spread, and potential outliers [7].

  2. Here is sample code to generate a boxplot of wt (Weight) of the cars. [3]

boxplot(tb$wt, 
        main = "Boxplot of Weight (wt)",
        ylab = "",
        xlab = "Weight ('000 kg)",
        col = "lightblue",
        horizontal = TRUE
       )

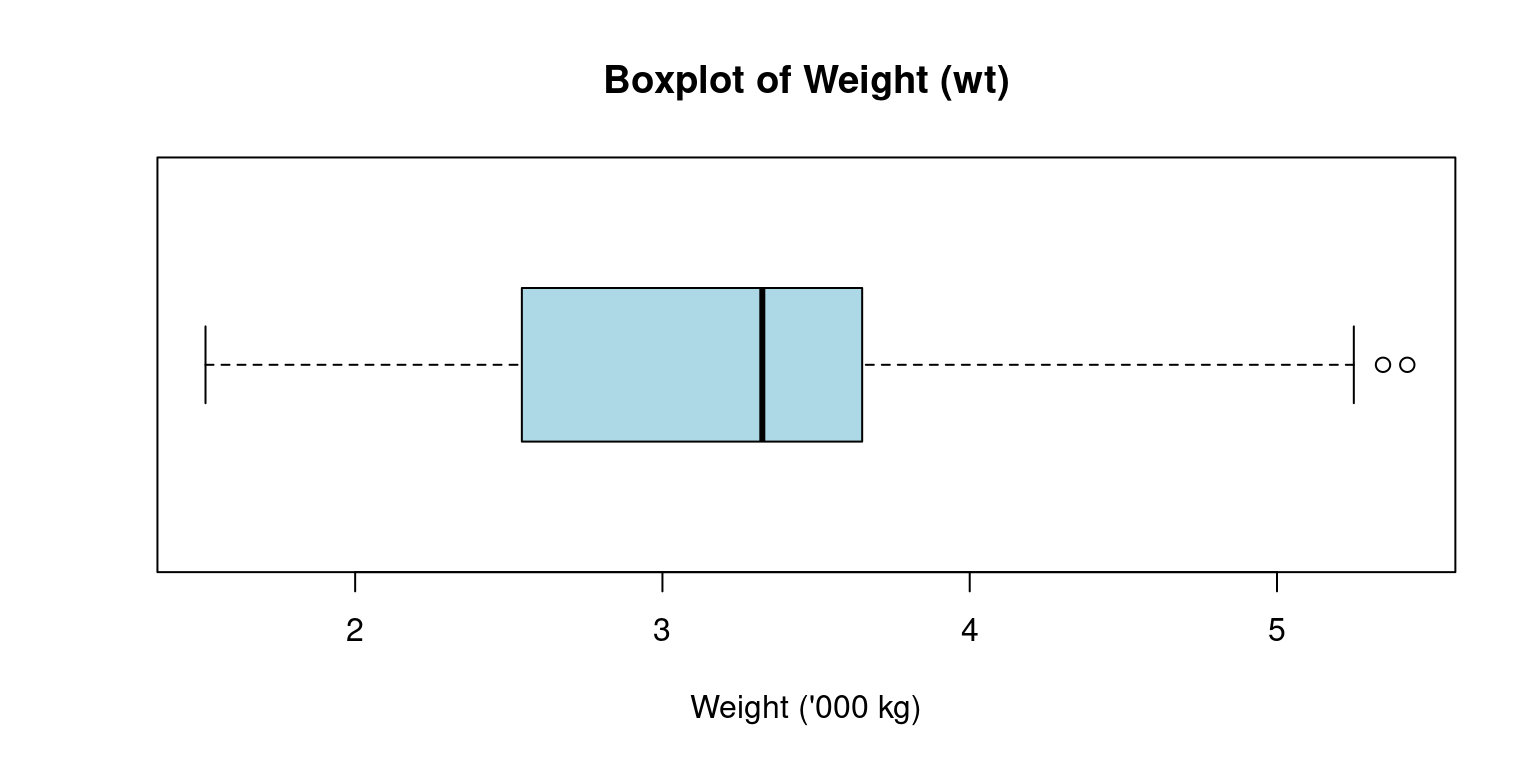
  1. The box plot’s construction involves the use of an interquartile range (IQR) represented by a box, which contains the middle 50% of the dataset, from Q1 to Q3.

  2. The box’s internal line signifies the median, while the “whiskers” reach out to the smallest and largest observations within a distance of 1.5 times the IQR.

  3. The whiskers extend to the minimum and maximum non-outlier values, or 1.5 times the interquartile range beyond the quartiles, whichever is shorter.

  4. Any points outside of the whiskers are considered outliers and are plotted individually.

  5. Discussion:

  • The above R code creates a horizontal light blue boxplot for the wt column of the tb data frame, titled “Boxplot of Weight (wt)”, with the x-axis labeled “Weight (’000 kg)” and no y-axis label.

  • horizontal = TRUE: Renders the boxplot horizontally rather than the default vertical orientation.

Violin Plot

  1. Violin plots are a compelling tool to merge the benefits of box plots and kernel density plots and enable us to depict a detailed view of data distribution.

  2. These plots exhibit the probability density at different values, where the plot’s breadth represents the density or frequency of data points. More extensive areas denote a higher aggregation of data points Akin to a box plot, a violin plot provides a visual display of the entire data distribution via a kernel density estimate, as opposed to just presenting the quartiles [8].

  3. The vioplot() function, part of the vioplot package in R, allows us to create a violin plot.

suppressPackageStartupMessages(library(vioplot))
# Constructing a violin plot for the wt
vioplot(tb$wt, 
        main="Violin Plot of Weight (wt)", 
        col = "lightblue",
        horizontal = TRUE,
        xlab="Weight"
        )

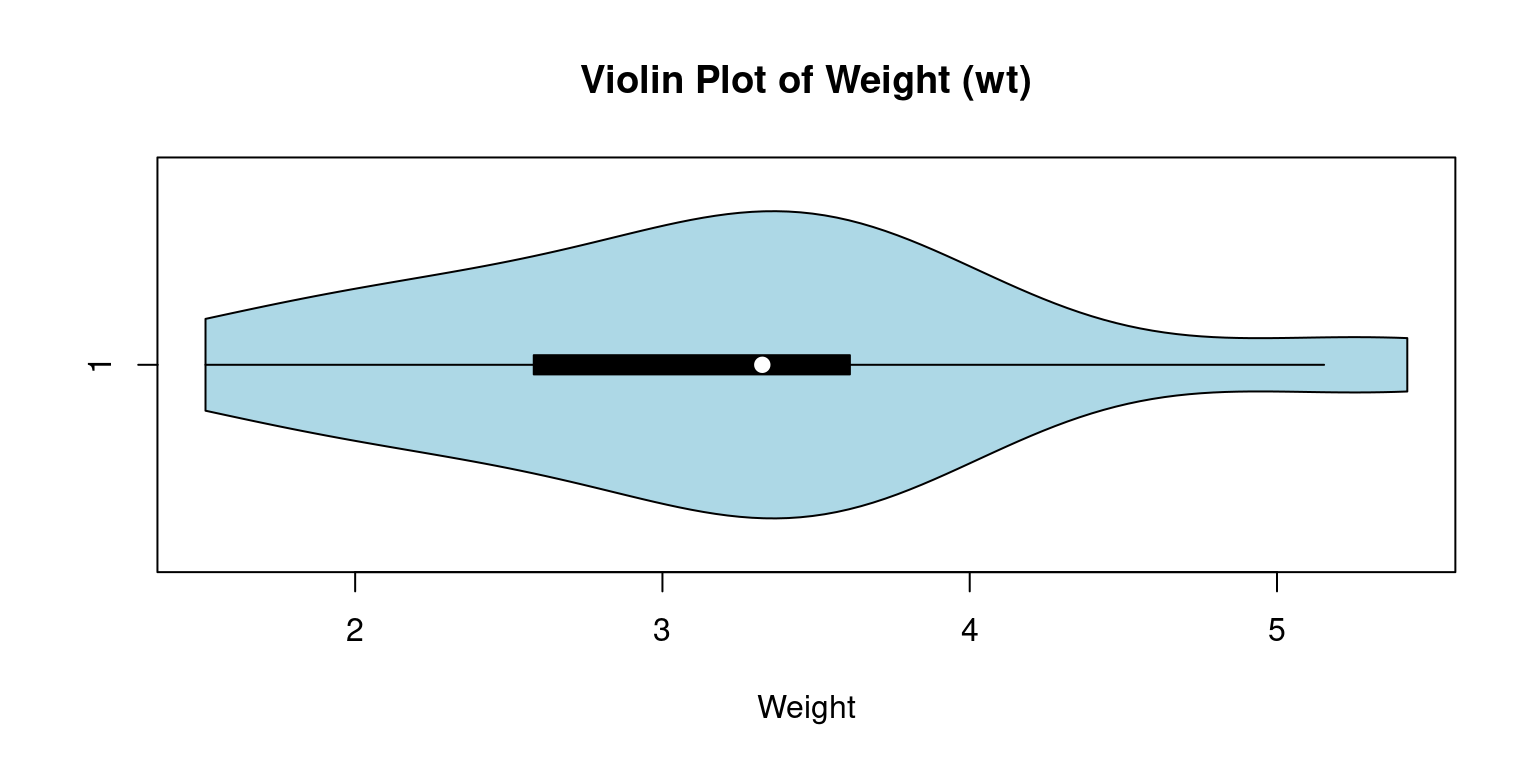
  1. Discussion:

  • In this code, the vioplot() function crafts a violin plot for the wt variable. We use the main argument to assign the plot’s title and the xlab argument to designate the axis label.

  • The resulting plot unveils the entire wt data distribution, with a kernel density estimate indicating the concentration of data points at different sections.

  • The plot also visualizes the boxplot and the median, quartiles, and any outliers present in the data.

  • horizontal = TRUE: Renders the violin plot horizontally rather than the default vertical orientation.

Quantile-Quantile (Q-Q) Plot

  1. Quantile-Quantile plots, commonly referred to as Q-Q plots, are a visual tool we use to check if data follows a particular distribution, like a normal distribution.

  2. Suppose we order a data column from the smallest to the biggest value, and each data point gets a score based on its position. This is what we call a quantile. Now, imagine a perfectly normal distribution doing the same thing. In a Q-Q plot, we compare our data’s scores to the scores from the ideal normal distribution.

  3. If our data aligns with the normal distribution, the points in the Q-Q plot will form a straight line. But if our data doesn’t follow the normal distribution, the points will stray from the line. This way, the Q-Q plot gives us an intuitive, visual way to decide if our data is normally distributed or not [3].

  4. In R, we can use the qqnorm() function to create the plot and the qqline() function to add the reference line. If the points lie close to the reference line, it’s a good indication that our data is normally distributed.

# Generate a Q-Q plot for 'mpg' column
qqnorm(tb$mpg)
# Add a reference line to the plot
qqline(tb$mpg)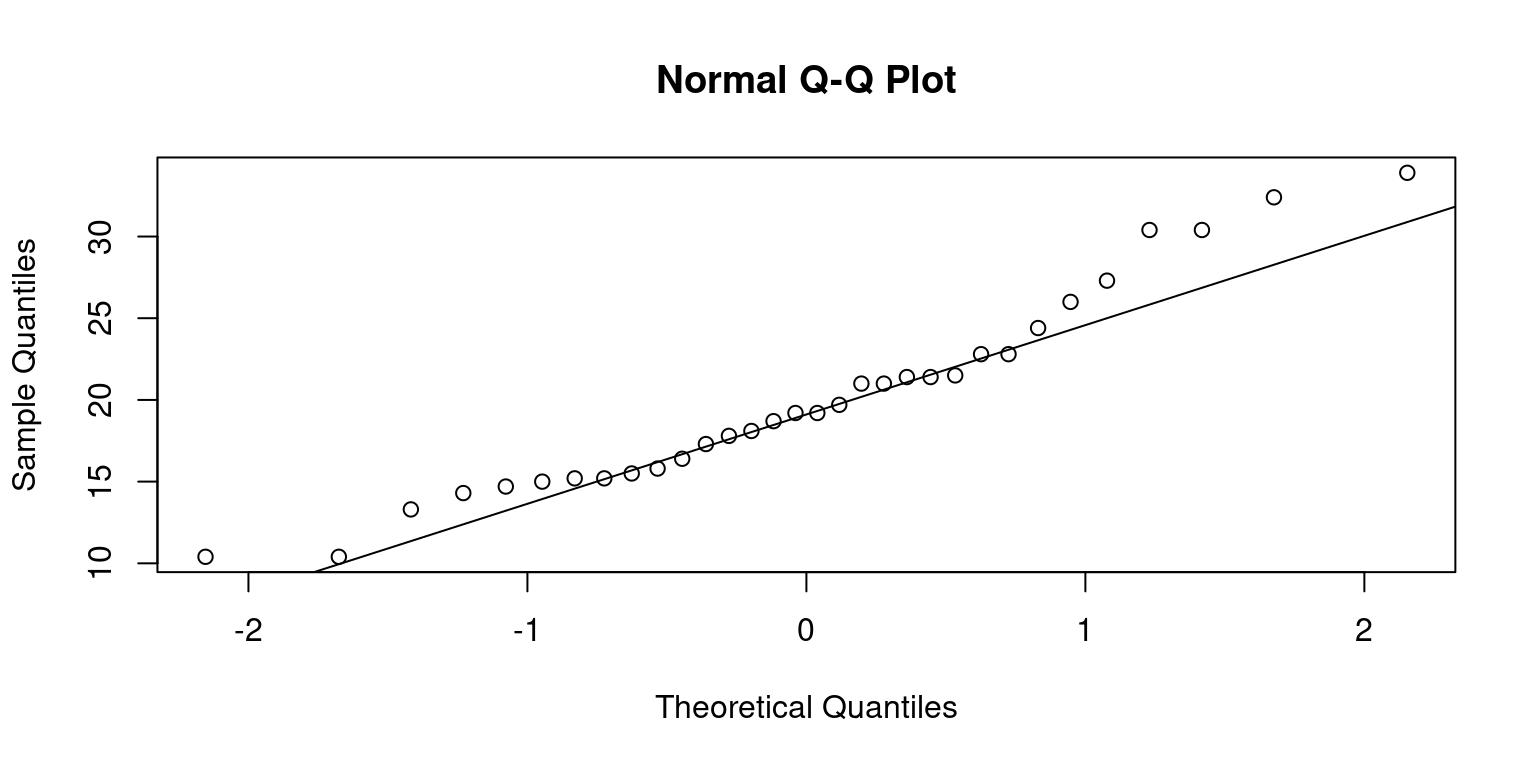

  1. This approach isn’t limited to normal distributions. We can compare our data with other distributions too, which makes Q-Q plots a versatile tool for understanding our data.

Summary of Chapter 10 – Univariate Continuous data (Part 1 of 2)

This chapter examines continuous univariate data, focusing on single variables in the ‘mtcars’ dataset using R’s dplyr and ggplot packages. We employ R’s inherent functions and the ‘modeest’ package to compute the mean, median, and mode, alongside variability measures like range, variance, and standard deviation.

We use R’s summary() and the psych package’s describe() functions to create succinct and detailed overviews of our data, providing insights into its central tendency, spread, and distribution shape. These functions can also summarize an entire dataframe or tibble, setting the stage for future analysis.

Visualisations are key to understanding data patterns and distributions. We use bee swarm plots, box plots, violin plots, histograms, and density plots. Bee swarm plots, using the beeswarm() function, show all data points and their distributions. Stem-and-leaf plots, created using the stem() function, provide a quick evaluation of the distribution.

Histograms, constructed with the hist() function, and density plots, using the density() function, display data frequency and smoothed approximations respectively. Cumulative Distribution Function (CDF) plots, via the ecdf() function, show the proportion of data points equal to or less than specific values.

Box plots, made with the boxplot function, highlight the distribution’s center, spread, and outliers. Violin plots, via the vioplot() function, merge box plots and kernel density plots to display data density. Lastly, Q-Q plots, created using qqnorm() and qqline(), verify if data follows a normal distribution.

To summarize, this chapter presents key R functions and techniques for visualizing continuous univariate data, providing valuable insights into data patterns and distributions.

References

R Programming:

[1] Crawley, M. J. (2007). The R Book. Wiley.

Kabacoff, R. I. (2015). R in Action: Data Analysis and Graphics with R (2nd ed.). Manning Publications.

R Core Team. (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Retrieved from https://www.R-project.org/.

Statistics:

[2] Bogaert, P. (2021). “A Comparison of Kernel Density Estimators.” Computational Statistics & Data Analysis, 77, 402-413.

Downey, A. B. (2014). Think Stats: Exploratory Data Analysis. O’Reilly Media.

Gravetter, F. J., & Wallnau, L. B. (2016). Statistics for the Behavioral Sciences. Cengage Learning.

Kleiber, C., & Zeileis, A. (2008). Applied Econometrics with R. Springer Science & Business Media.

Moore, D. S., McCabe, G. P., & Craig, B. A. (2012). Introduction to the Practice of Statistics. Freeman.

Triola, M. (2017). Elementary Statistics. Pearson.

Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.

Thode Jr, H. C. (2002). Testing for Normality. CRC Press.

Venables, W. N., & Ripley, B. D. (2002). Modern Applied Statistics with S (4th ed.). Springer.

Statistics using R:

[3] Field, A., Miles, J., & Field, Z. (2012). Discovering Statistics Using R. Sage Publications.

R Core Team. (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Retrieved from https://www.R-project.org/.

Hyndman, R. J., & Fan, Y. (1996). Sample Quantiles in Statistical Packages. The American Statistician, 50(4), 361-365.

psych:

[4] Revelle, W. (2020). psych: Procedures for Psychological, Psychometric, and Personality Research. Northwestern University, Evanston, Illinois. R Package Version 2.0.12. Retrieved from https://CRAN.R-project.org/package=psych.

Beeswarm:

[5] Ellis, K. (2011). Beeswarm: The Bee Swarm Plot, an Alternative to Stripchart. R Package Version 0.2.3.

Histograms:

[6] Scott, D. W. (1979). On Optimal and Data-Based Histograms. Biometrika, 66(3), 605-610.

Wand, M. P., & Jones, M. C. (1995). Kernel Smoothing. Chapman and Hall/CRC.

Boxplots:

[7] McGill, R., Tukey, J. W., & Larsen, W. A. (1978). Variations of Box Plots. The American Statistician, 32(1), 12-16.

Violin Plots:

[8] Hintze, J. L., & Nelson, R. D. (1998). Violin Plots: A Box Plot-Density Trace Synergism. The American Statistician, 52(2), 181-184.